
【题目】如图所示,在四棱台![]() 中,
中,![]() 底面
底面![]() ,四边形
,四边形![]() 为菱形,
为菱形,![]() ,
,![]() .
.
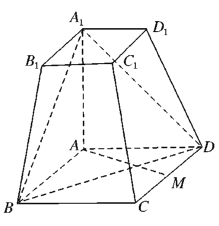
(1)若![]() 为
为![]() 中点,求证:
中点,求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
试题(1)连接![]() ,可证
,可证![]() ,又因为
,又因为![]() 底面
底面![]() ,可得
,可得![]() ,即可得证.
,即可得证.
(2)如图建立空间直角坐标系![]() ,求出
,求出![]() 和平面
和平面![]() 的一个法向量
的一个法向量![]() 的坐标,则直线
的坐标,则直线![]() 与平面
与平面![]() 所成角的正弦值
所成角的正弦值![]() .
.
试题解析:
(Ⅰ)∵四边形![]() 为菱形,
为菱形,![]() ,连结
,连结![]() ,则
,则![]() 为等边三角形,
为等边三角形,
又∵![]() 为
为![]() 中点∴
中点∴![]() ,由
,由![]() 得∴
得∴![]()
∵![]() 底面
底面![]() ,
,![]() 底面
底面![]() ∴
∴![]() ,又∵
,又∵![]()
∴![]() 平面
平面![]()
(Ⅱ)∵四边形![]() 为菱形,
为菱形,![]() ,
,![]() ,
,
得![]() ,
,![]() ,∴
,∴![]() 又∵
又∵![]() 底面
底面![]() ,
,
分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系![]()
![]() 、
、![]() 、
、![]() 、
、![]()
∴![]() ,
,![]() ,
,![]()
设平面![]() 的一个法向量
的一个法向量![]() ,
,
则有 ,令
,令![]() ,则
,则![]()
∴直线![]() 与平面
与平面![]() 所成角
所成角![]() 的正弦值
的正弦值
 .
.

点晴:本题考查的空间的线面关系以及空间的角.第一问通过证明直线![]() 和平面
和平面![]() 内的两条相交直线
内的两条相交直线![]() 垂直,证明
垂直,证明![]() 平面
平面![]() ;第二问中通过建立空间直角坐标系
;第二问中通过建立空间直角坐标系![]() ,求得
,求得![]() 和平面
和平面![]() 的一个法向量
的一个法向量![]()
,结合![]() 得到结论.
得到结论.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,过点
,过点![]() 的直线与抛物线交于
的直线与抛物线交于![]() 两点,又过
两点,又过![]() 两点分别作抛物线的切线,两条切线交于
两点分别作抛物线的切线,两条切线交于![]() 点。
点。
(1)证明:直线![]() 的斜率之积为定值;
的斜率之积为定值;
(2)求![]() 面积的最小值
面积的最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=2sin(ωx+φ)(ω>0,|φ|<![]() )的一个零点为
)的一个零点为![]() ,其图象距离该零点最近的一条对称轴为x=
,其图象距离该零点最近的一条对称轴为x=![]() .
.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若关于x的方程f(x)+log2k=0在x∈[![]() ,
,![]() ]上恒有实数解,求实数k的取值范围.
]上恒有实数解,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥PABCD中,PA⊥底面ABCD,AD∥BC,AB=AC=AD=3,PA=BC=4.
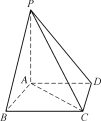
(1)求异面直线PB与CD所成角的余弦值;
(2)求平面PAD与平面PBC所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新高考3+3最大的特点就是取消文理科,除语文、数学、外语之外,从物理、化学、生物、政治、历史、地理这6科中自由选择三门科目作为选考科目.某研究机构为了了解学生对全理(选择物理、化学、生物)的选择是否与性别有关,觉得从某学校高一年级的650名学生中随机抽取男生,女生各25人进行模拟选科.经统计,选择全理的人数比不选全理的人数多10人.
(1)请完成下面的2×2列联表;
选择全理 | 不选择全理 | 合计 | |
男生 | 5 | ||
女生 | |||
合计 |
(2)估计有多大把握认为选择全理与性别有关,并说明理由;
(3)现从这50名学生中已经选取了男生3名,女生2名进行座谈,从中抽取2名代表作问卷调查,求至少抽到一名女生的概率.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附: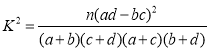 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)= 的图象在点(-2,f (-2))处的切线方程为16x+y+20=0.
的图象在点(-2,f (-2))处的切线方程为16x+y+20=0.
(1)求实数a、b的值;
(2)求函数f(x)在区间[-1,2]上的最大值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正整数数列中,由1开始依次按如下规则取到的项:第一次取1;第二次取2个连续的偶数2,4;第三次取3个连续的奇数5,7,9:第四次取4个连续的偶数10,12,14,16……按此规律一直取下去,得到一个子数列1,2,4,5,7,9,10,12,14,16…,则在这个子数列中,第2014个数是( )
A.3965B.3966C.3968D.3969
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,过原点
,过原点![]() 且斜率为1的直线交椭圆
且斜率为1的直线交椭圆![]() 于
于![]() 两点,四边形
两点,四边形![]() 的周长与面积分别为12与
的周长与面积分别为12与![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() 与圆
与圆![]() 相切,且与椭圆
相切,且与椭圆![]() 交于
交于![]() 两点,求原点到
两点,求原点到![]() 的中垂线的最大距离.
的中垂线的最大距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com