
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<![]() )在某一个周期内的图象时,列表并填入了部分数据,如表:
)在某一个周期内的图象时,列表并填入了部分数据,如表:
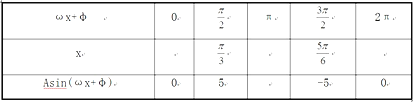
(1)请将上表数据补充完整,并直接写出函数f(x)的解析式.
(2)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g(x)的图象.若y=g(x)图象的一个对称中心为![]() ,求θ的最小值.
,求θ的最小值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)在区间![]() 上画出函数
上画出函数![]() 的图象;
的图象;
(2)设集合![]() ,
,![]() .试判断集合
.试判断集合![]() 和
和![]() 之间的关系,并给出证明;
之间的关系,并给出证明;
(3)当![]() 时,求证:在区间
时,求证:在区间![]() 上,
上,![]() 的图象位于函数
的图象位于函数![]() 图象的上方.
图象的上方.
查看答案和解析>>
科目:高中数学 来源: 题型:
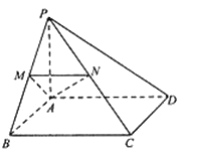
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,四边形
,四边形![]() 为正方形,点
为正方形,点![]() 分别为线段
分别为线段![]() 上的点,
上的点,![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求证:当点![]() 不与点
不与点![]() 重合时,
重合时,![]() 平面
平面![]() ;
;
(3)当![]() 时,求点
时,求点![]() 到直线
到直线![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元。该公司第n年需要付出设备的维修和工人工资等费用![]() 的信息如下图。
的信息如下图。
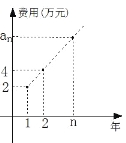
(Ⅰ)求![]() ;
;
(Ⅱ)引进这种设备后,第几年后该公司开始获利;
(Ⅲ)这种设备使用多少年,该公司的年平均获利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在数列{an}中,Sn为其前n项和,若an>0,且4Sn=an2+2an+1(n∈N*),数列{bn}为等比数列,公比q>1,b1=a1,且2b2,b4,3b3成等差数列.
(1)求{an}与{bn}的通项公式;
(2)令cn=![]() ,若{cn}的前项和为Tn,求证:Tn<6.
,若{cn}的前项和为Tn,求证:Tn<6.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若函数![]() 的图象在点
的图象在点![]() 处的切线的倾斜角为
处的切线的倾斜角为![]() ,且函数
,且函数![]() 当且仅当在
当且仅当在![]() 处取得极值,其中
处取得极值,其中![]() 为
为![]() 的导函数,求
的导函数,求![]() 的取值范围;
的取值范围;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com