练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】是坐标原点，椭圆：的左右焦点分别为，，点在椭圆上，若的面积最大时且最大面积为.

    （1）求椭圆的标准方程；

    （2）直线：与椭圆在第一象限交于点，点是第四象限内的点且在椭圆上，线段被直线垂直平分，直线与椭圆交于另一点，求证：.

    【答案】（1）；

    （2）证明见解析.

    【解析】

    （1）由的面积最大时且最大面积为求得且，再结合即可求出椭圆的标准方程；（2）易知，设直线：，则直线：，然后分别与联立求出，，再利用斜率公式得出的值即可.

    （1）当是椭圆的上顶点或下顶点时的面积最大，设是椭圆的上顶点，

    则即，

    又，∴，，，

    ∴椭圆的标准方程为.

    （2）依题意点的坐标为，直线不与垂直，设直线：，

    即，直线：，即，

    设，，

    由得，

    ∴，∴，

    则.

    又，，

    ∴，

    又，∴，

    ∴.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

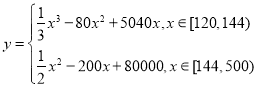    【题目】某公司为了变废为宝，节约资源，新上了一个从生活垃圾中提炼生物柴油的项目．经测算该项目月处理成本（元）与月处理量（吨）之间的函数关系可以近似地表示为：，且每处理一吨生活垃圾，可得到能利用的生物柴油价值为元，若该项目不获利，政府将给予补贴．

    （1）当时，判断该项目能否获利？如果获利，求出最大利润；如果不获利，则政府每月至少需要补贴多少元才能使该项目不亏损？

    （2）该项目每月处理量为多少吨时，才能使每吨的平均处理成本最低？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知a，b，c分别为△ABC三个内角A，B，C的对边，且acos C＋asin C－b－c＝0.

    (1)求A；

    (2)若AD为BC边上的中线，cos B＝，AD＝，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （Ⅰ）讨论的单调性；

    （Ⅱ）若，求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数．

    （1）若曲线在点处的切线与轴垂直，求实数的值；

    （2）若在处取得极大值，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】海洋蓝洞是地球罕见的自然地理现象，被喻为“地球留给人类保留宇宙秘密的最后遗产”，我国拥有世界上最深的海洋蓝洞，若要测量如图所示的蓝洞的口径，两点间的距离，现在珊瑚群岛上取两点，，测得，，，，则，两点的距离为___．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示的几何体中，．

    (1)求证：平面ABCD；

    (2)若，点F在EC上，且满足EF=2FC，求二面角F—AD—C的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    (1)求函数的单调区间与极值.

    (2)当时，是否存在，使得成立？若存在，求实数的取值范围，若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】双曲线经过点，两条渐近线的夹角为，直线交双曲线于、.

    （1）求双曲线的方程；

    （2）若过原点，为双曲线上异于、的一点，且直线、的斜率为、，证明：为定值；

    （3）若过双曲线的右焦点，是否存在轴上的点，使得直线绕点无论怎样转动，都有成立？若存在，求出的坐标，若不存在，请说明理由.

    查看答案和解析>>

    同步练习册答案