
【题目】(1)若函数![]() 的图象在
的图象在![]() 处的切线
处的切线![]() 垂直于直线
垂直于直线![]() ,求实数
,求实数![]() 的值及直线
的值及直线![]() 的方程;
的方程;
(2)求函数![]() 的单调区间;
的单调区间;
(3)若![]() ,求证:
,求证: ![]() .
.
【答案】(1)![]() ,
, ![]() ;(2)当
;(2)当![]() 时,
时, ![]() 的单调递增区间是
的单调递增区间是![]() ;当
;当![]() 时,
时, ![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】试题分析:(1)求出函数的导数,根据切线的斜率求出![]() 的值,从而求出函数的切点,点斜式求出切线方程即可;(2)求出
的值,从而求出函数的切点,点斜式求出切线方程即可;(2)求出![]() ,分别令
,分别令 ![]() 得增区间,
得增区间, ![]() 得减区间;(3)由
得减区间;(3)由![]() 时,
时, ![]() ,在
,在![]() 上单调递减,得到
上单调递减,得到![]() ,从而证明结论.
,从而证明结论.
试题解析:(1)∵![]() (
(![]() ),定义域为
),定义域为![]() ,∴
,∴![]()
∴函数![]() 的图象在
的图象在![]() 处的切线
处的切线![]() 的斜率
的斜率![]()
∵切线![]() 垂直于直线
垂直于直线![]() ,∴
,∴![]() ,∴
,∴![]()
∴![]() ,
, ![]() ,∴切点为
,∴切点为![]()
∴切线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
(2)由(1)知: ![]() ,
, ![]()
当![]() 时,
时, ![]() ,此时
,此时![]() 的单调递增区间是
的单调递增区间是![]() ;
;
当![]() 时,
时, ![]()
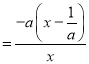
若![]() ,则
,则![]() ;若
;若![]() ,则
,则![]()
此时![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]()
综上所述:
当![]() 时,
时, ![]() 的单调递增区间是
的单调递增区间是![]() ;
;
当![]() 时,
时, ![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]() .
.
(3)由(2)知:当![]() 时,
时, ![]() 在
在![]() 上单调递减
上单调递减
∴![]() 时,
时, ![]()
∴![]() 时,
时, ![]() ,即
,即![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0),其部分图象如图所示,点P,Q分别为图象上相邻的最高点与最低点,R是图象与x轴的交点,若P点的横坐标为 ![]() ,f(
,f( ![]() )=
)= ![]() ,PR⊥QR,则函数f(x)的解析式可以是( )
,PR⊥QR,则函数f(x)的解析式可以是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱A1B1C1﹣ABC中, ![]() ,AB=AC=AA1=1,已知G和E分别为A1B1和CC1的中点,D与F分别为线段AC和AB上的动点(不包括端点),若GD⊥EF,则线段DF的长度的取值范围为( )
,AB=AC=AA1=1,已知G和E分别为A1B1和CC1的中点,D与F分别为线段AC和AB上的动点(不包括端点),若GD⊥EF,则线段DF的长度的取值范围为( )
A.[ ![]() ,1)
,1)
B.[ ![]() ,1]
,1]
C.( ![]() ,1)
,1)
D.[ ![]() ,1)
,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国“一带一路”战略构思提出后, 某科技企业为抓住“一带一路”带来的机遇, 决定开发生产一款大型电子设备, 生产这种设备的年固定成本为![]() 万元, 每生产
万元, 每生产![]() 台,需另投入成本
台,需另投入成本![]() (万元), 当年产量不足
(万元), 当年产量不足![]() 台时,
台时,![]() (万元); 当年产量不小于
(万元); 当年产量不小于![]() 台时
台时![]() (万元), 若每台设备售价为
(万元), 若每台设备售价为![]() 万元, 通过市场分析,该企业生产的电子设备能全部售完.
万元, 通过市场分析,该企业生产的电子设备能全部售完.
(1)求年利润![]() (万元)关于年产量
(万元)关于年产量![]() (台)的函数关系式;
(台)的函数关系式;
(2)年产量为多少台时 ,该企业在这一电子设备的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1 , F2分别为双曲线C: ![]() ﹣
﹣ ![]() =1的左、右焦点,若存在过F1的直线分别交双曲线C的左、右支于A,B两点,使得∠BAF2=∠BF2F1 , 则双曲线C的离心率e的取值范围是( )
=1的左、右焦点,若存在过F1的直线分别交双曲线C的左、右支于A,B两点,使得∠BAF2=∠BF2F1 , 则双曲线C的离心率e的取值范围是( ) 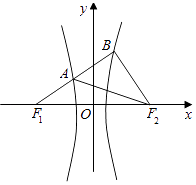
A.(3,+∞)
B.(1,2+ ![]() )
)
C.(3,2+ ![]() )
)
D.(1,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项为和Sn , 点(n, ![]() )在直线y=
)在直线y= ![]() x+
x+ ![]() 上.数列{bn}满足bn+2﹣2bn+1+bn=0(n∈N*),且b3=11,前9项和为153.
上.数列{bn}满足bn+2﹣2bn+1+bn=0(n∈N*),且b3=11,前9项和为153.
(1)求数列{an},{bn}的通项公式;
(2)求数列 ![]() 的前n项和Tn
的前n项和Tn
(3)设n∈N* , f(n)= ![]() 问是否存在m∈N* , 使得f(m+15)=5f(m)成立?若存在,求出m的值;若不存在,请说明理由.
问是否存在m∈N* , 使得f(m+15)=5f(m)成立?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com