
【题目】已知函数![]() .
.
(1)当![]() 时,求证:
时,求证:![]() 在
在![]() 上是单调递减函数;
上是单调递减函数;
(2)若函数![]() 有两个正零点
有两个正零点![]() 、
、![]() ,求
,求![]() 的取值范围,并证明:
的取值范围,并证明:![]() .
.
【答案】(1)见证明;(2)实数![]() 的取值范围是
的取值范围是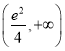 ,证明见解析.
,证明见解析.
【解析】
(1)由题意得出![]() 在区间
在区间![]() 上恒成立,由
上恒成立,由![]() 得出
得出![]()
![]() ,构造函数
,构造函数![]() ,证明
,证明![]() 在区间
在区间![]() 上恒成立即可;
上恒成立即可;
(2)由![]() 利用参变量分离法得出
利用参变量分离法得出![]() ,将题意转化为当直线
,将题意转化为当直线![]() 与函数
与函数![]() 在
在![]() 上有两个交点时求
上有两个交点时求![]() 的取值范围,利用数形结合思想求解即可,然后由题意得出
的取值范围,利用数形结合思想求解即可,然后由题意得出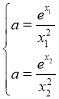 ,取自然对数得
,取自然对数得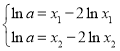 ,等式作差得
,等式作差得![]() ,利用分析得出所证不等式等价于
,利用分析得出所证不等式等价于![]() ,然后构造函数
,然后构造函数![]() 证明即可.
证明即可.
(1)![]() ,
,![]() .
.
由题意知,不等式![]() 在区间
在区间![]() 上恒成立,
上恒成立,
由于![]() ,当
,当![]() 时,
时,![]() ,
,
构造函数![]() ,其中
,其中![]() ,则
,则![]() ,令
,令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以,函数![]() 在
在![]() 处取得极大值,亦即最大值,即
处取得极大值,亦即最大值,即![]() ,
,
![]() ,所以,
,所以,![]() .
.
所以,不等式![]() 在区间
在区间![]() 上恒成立,
上恒成立,
因此,当![]() 时,函数
时,函数![]() 在
在![]() 上是单调递减函数;
上是单调递减函数;
(2)令![]() ,可得
,可得![]()
令![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
当![]() 时,函数
时,函数![]() 单调递减,当
单调递减,当![]() 时,函数
时,函数![]() 单调递增.
单调递增.
![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时.
时.![]() .
.
![]() 时,函数
时,函数![]() 有两个正零点,因此,实数
有两个正零点,因此,实数![]() 的取值范围是
的取值范围是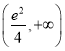 .
.
由上知![]() 时,
时,![]() ,
,
由题意得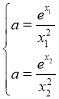 ,上述等式两边取自然对数得
,上述等式两边取自然对数得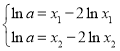 ,
,
两式作差得![]() ,
,![]() ,
,
要证![]() ,即证
,即证![]() .
.
由于![]() ,则
,则![]() ,即证
,即证![]() ,
,
即证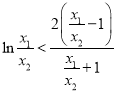 ,令
,令![]() ,即证
,即证![]() ,其中
,其中![]() .
.
构造函数![]() ,其中
,其中![]() ,即证
,即证![]() 在
在![]() 上恒成立.
上恒成立.
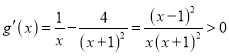 ,所以,函数
,所以,函数![]() 在区间
在区间![]() 上恒成立,
上恒成立,
所以,![]() ,因此,
,因此,![]() .
.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】从集合![]() 的所有非空子集中,等可能地取出
的所有非空子集中,等可能地取出![]() 个.
个.
(1)若![]() ,求所取子集的元素既有奇数又有偶数的概率;
,求所取子集的元素既有奇数又有偶数的概率;
(2)若![]() ,记所取子集的元素个数之差为
,记所取子集的元素个数之差为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在国庆![]() 周年庆典活动中,东城区教育系统近
周年庆典活动中,东城区教育系统近![]() 名师生参与了国庆中心区合唱、
名师生参与了国庆中心区合唱、![]() 方阵群众游行、联欢晚会及
方阵群众游行、联欢晚会及![]() 万只气球保障等多项重点任务.设
万只气球保障等多项重点任务.设![]() 是参与国庆中心区合唱的学校
是参与国庆中心区合唱的学校![]() ,
,![]() 是参与27方阵群众游行的学校
是参与27方阵群众游行的学校![]() ,
,![]() 是参与国庆联欢晚会的学校
是参与国庆联欢晚会的学校![]() .请用上述集合之间的运算来表示:①既参与国庆中心区合唱又参与27方阵群众游行的学校的集合为_____;②至少参与国庆中心区合唱与国庆联欢晚会中一项的学校的集合为_____.
.请用上述集合之间的运算来表示:①既参与国庆中心区合唱又参与27方阵群众游行的学校的集合为_____;②至少参与国庆中心区合唱与国庆联欢晚会中一项的学校的集合为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在D上的函数f(x)如果满足:对任意x∈D,存在常数M≥0,都有|f(x)|≤M成立,则称f(x)是D上的有界函数,其中M称为函数f(x)的一个上界.已知函数![]() ,
,![]() .
.
(1)求函数f(x)在区间![]() 上的所有上界构成的集合;
上的所有上界构成的集合;
(2)若函数g(x)在[0,+∞)上是以7为上界的有界函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数z=![]() 2016+(1-i)2(其中i为虚数单位),若复数z的共轭复数为
2016+(1-i)2(其中i为虚数单位),若复数z的共轭复数为![]() ,且
,且![]() ·z1=4+3i.
·z1=4+3i.
(1)求复数z1;
(2)若z1是关于x的方程x2-px+q=0的一个根,求实数p,q的值,并求出方程x2-px+q=0的另一个复数根.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的相邻两对称轴间的距离为
的相邻两对称轴间的距离为![]() ,若将
,若将![]() 的图像先向左平移
的图像先向左平移![]() 个单位,再向下平移
个单位,再向下平移![]() 个单位,所得的函数
个单位,所得的函数![]() 为奇函数.
为奇函数.
(1)求![]() 的解析式;
的解析式;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不等实根,求实数
上有两个不等实根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)某学校为了支持生物课程基地研究植物生长,计划利用学校空地建造一间室内面积为900m2的矩形温室,在温室内划出三块全等的矩形区域,分别种植三种植物,相邻矩形区域之间间隔1m,三块矩形区域的前、后与内墙各保留 1m 宽的通道,左、右两块矩形区域分别与相邻的左右内墙保留 3m 宽的通道,如图.设矩形温室的室内长为![]() (m),三块种植植物的矩形区域的总面积为
(m),三块种植植物的矩形区域的总面积为![]() (m2).
(m2).

(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为![]() ,其范围为
,其范围为![]() ,分为五个级别,
,分为五个级别, ![]() 畅通;
畅通; ![]() 基本畅通;
基本畅通; ![]() 轻度拥堵;
轻度拥堵; ![]() 中度拥堵;
中度拥堵; ![]() 严重拥堵.早高峰时段(
严重拥堵.早高峰时段(![]() ),从某市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如图.
),从某市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如图.

(1)这50个路段为中度拥堵的有多少个?
(2)据此估计,早高峰三环以内的三个路段至少有一个是严重拥堵的概率是多少?
(3)某人上班路上所用时间若畅通时为20分钟,基本畅通为30分钟,轻度拥堵为36分钟,中度拥堵为42分钟,严重拥堵为60分钟,求此人所用时间的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为庆祝党的98岁生日,某高校组织了“歌颂祖国,紧跟党走”为主题的党史知识竞赛。从参加竞赛的学生中,随机抽取40名学生,将其成绩分为六段![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,到如图所示的频率分布直方图.
,到如图所示的频率分布直方图.

(1)求图中![]() 的值及样本的中位数与众数;
的值及样本的中位数与众数;
(2)若从竞赛成绩在![]() 与
与![]() 两个分数段的学生中随机选取两名学生,设这两名学生的竞赛成绩之差的绝对值不大于
两个分数段的学生中随机选取两名学生,设这两名学生的竞赛成绩之差的绝对值不大于![]() 分为事件
分为事件![]() ,求事件
,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com