
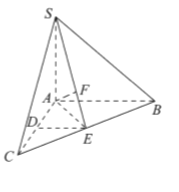
【题目】如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,![]() E是PD的中点.
E是PD的中点.
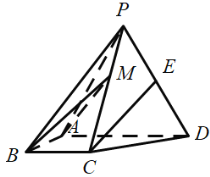
(1)证明:直线![]() 平面PAB;
平面PAB;
(2)点M在棱PC 上,且直线BM与底面ABCD所成角为![]() ,求二面角M-AB-D的余弦值.
,求二面角M-AB-D的余弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)取PA的中点F,连接EF,BF,通过证明CE∥BF,利用直线与平面平行的判定定理证明即可;
(2)利用已知条件转化求解M到底面的距离,作出二面角的平面角,然后求解二面角MABD的余弦值即可.
(1)证明:取PA的中点F,连接EF,BF,
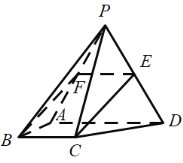
因为E是PD的中点,
所以![]() ,∠BAD=∠ABC=90°,
,∠BAD=∠ABC=90°,
∴![]() ,
,
∴BCEF是平行四边形,可得CE∥BF,BF平面PAB,![]() 平面PAB,
平面PAB,
∴直线CE∥平面PAB;
(2)解:四棱锥PABCD中,
侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=![]() AD,
AD,
∠BAD=∠ABC=90°,E是PD的中点.
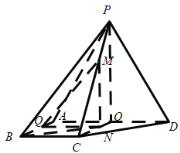
取AD的中点O,M在底面ABCD上的射影N在OC上,
设AD=2,则AB=BC=1,OP=![]() ,
,
∴∠PCO=60°,直线BM与底面ABCD所成角为45°,
可得:BN=MN,![]() ,BC=1,
,BC=1,
可得:![]() ,
,
作NQ⊥AB于Q,连接MQ,AB⊥MN,
所以∠MQN就是二面角MABD的平面角,MQ= ,
,
二面角MABD的余弦值为: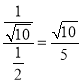 .
.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:高中数学 来源: 题型:
【题目】2019年4月,北京世界园艺博览会开幕,为了保障园艺博览会安全顺利地进行,某部门将5个安保小组全部安排到指定的三个不同区域内值勤,则每个区域至少有一个安保小组的排法有( )
A.150种B.240种C.300种D.360种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() 在
在![]() 上且
上且![]() .
.
(I)求证:![]() ;
;
(II)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(III)在线段![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆![]() 与圆
与圆![]() :
: ![]() 相切,且与圆
相切,且与圆![]() :
: ![]() 相内切,记圆心
相内切,记圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .设
.设![]() 为曲线
为曲线![]() 上的一个不在
上的一个不在![]() 轴上的动点,
轴上的动点, ![]() 为坐标原点,过点
为坐标原点,过点![]() 作
作![]() 的平行线交曲线
的平行线交曲线![]() 于
于![]() ,
, ![]() 两个不同的点.
两个不同的点.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)试探究![]() 和
和![]() 的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
的比值能否为一个常数?若能,求出这个常数,若不能,请说明理由;
(Ⅲ)记![]() 的面积为
的面积为![]() ,
, ![]() 的面积为
的面积为![]() ,令
,令![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】英语老师要求学生从星期一到星期四每天学习3个英语单词:每周五对一周内所学单词随机抽取若干个进行检测(一周所学的单词每个被抽到的可能性相同)
(1)英语老师随机抽了![]() 个单词进行检测,求至少有
个单词进行检测,求至少有![]() 个是后两天学习过的单词的概率;
个是后两天学习过的单词的概率;
(2)某学生对后两天所学过的单词每个能默写对的概率为![]() ,对前两天所学过的单词每个能默写对的概率为
,对前两天所学过的单词每个能默写对的概率为![]() ,若老师从后三天所学单词中各抽取一个进行检测,求该学生能默写对的单词的个数
,若老师从后三天所学单词中各抽取一个进行检测,求该学生能默写对的单词的个数![]() 的分布列和期望。
的分布列和期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于顶点在原点的抛物线,给出下列条件:
①焦点在y轴上;
②焦点在x轴上
③抛物线上横坐标为1的点到焦点的距离等于6;
④抛物线的过焦点且垂直于对称轴的弦的长为5;
⑤由原点向过焦点的某条直线作垂线,垂足坐标为(2,1)
能使抛物线方程为y2=10x的条件是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com