
【题目】已知函数![]()
![]() 讨论函数
讨论函数![]() 的单调性;
的单调性;
![]() 当
当![]() 时,求函数
时,求函数![]() 在区间
在区间![]() 上的零点个数.
上的零点个数.
【答案】(1)见解析;(2)见解析
【解析】
(1)先对函数![]() 求导,分别讨论
求导,分别讨论![]() ,
,![]() ,即可得出结果;
,即可得出结果;
(2)先由(1)得![]() 时,函数
时,函数![]() 的最大值
的最大值![]() ,分别讨论
,分别讨论![]() ,
,![]() ,
,![]() ,即可结合题中条件求出结果.
,即可结合题中条件求出结果.
解:(1)![]()
![]() ,
,![]()
![]() ,
,
![]()
![]()
当![]() 时,
时,![]() ,
,
当![]() 时,
时,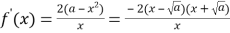 ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]() 当
当![]() 时,
时,![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2)由(1)得![]() ,
,
当![]() ,即
,即![]() 时,函数
时,函数![]() 在
在![]() 内有无零点;
内有无零点;
当![]() ,即
,即![]() 时,函数
时,函数![]() 在
在![]() 内有唯一零点
内有唯一零点![]() ,
,
又![]() ,所以函数
,所以函数![]() 在
在![]() 内有一个零点;
内有一个零点;
当![]() ,即
,即![]() 时,由于
时,由于![]() ,
,![]() ,
,
![]() ,
,
若![]() ,即
,即![]() 时,
时,![]() ,由函数单调性知
,由函数单调性知
![]() 使得
使得![]() ,
,![]() 使得
使得![]() ,
,
故此时函数![]() 在
在![]() 内有两个零点;
内有两个零点;
若![]() ,即
,即![]() 时,
时,![]() ,
,
且![]() ,
,![]() ,
,
由函数的单调性可知![]() 在
在![]() 内有唯一的零点,在
内有唯一的零点,在![]() 内没有零点,从而
内没有零点,从而![]() 在
在![]() 内只有一个零点
内只有一个零点
综上所述,当![]() 时,函数
时,函数![]() 在
在![]() 内有无零点;
内有无零点;
当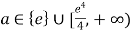 时,函数
时,函数![]() 在
在![]() 内有一个零点;
内有一个零点;
当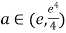 时,函数
时,函数![]() 在
在![]() 内有两个零点.
内有两个零点.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 且
且![]() ).
).
(1)判断函数![]() 的奇偶性并说明理由;
的奇偶性并说明理由;
(2)当![]() 时,判断函数
时,判断函数![]() 在
在![]() 上的单调性,并利用单调性的定义证明;
上的单调性,并利用单调性的定义证明;
(3)是否存在实数![]() ,使得当
,使得当![]() 的定义域为
的定义域为![]() 时,值域为
时,值域为![]() ?若存在,求出实数
?若存在,求出实数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
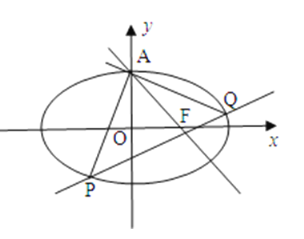
【题目】如图,已知椭圆![]() 的上顶点为
的上顶点为![]() ,右焦点为
,右焦点为![]() ,直线
,直线![]() 与圆
与圆![]() 相切.
相切.
(1)求椭圆![]() 的方程;
的方程;
(2)不过点![]() 的动直线
的动直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,且
两点,且![]() .求证:直线
.求证:直线![]() 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】耐盐碱水稻俗称“海水稻”,是一种可以长在滩涂和盐碱地的水稻。还水稻的灌溉是将海水稀释后进行灌溉。某实验基础为了研究海水浓度![]() (
(![]() )对亩产量
)对亩产量![]() (吨)的影响,通过在试验田的种植实验,测得了某种还水稻的亩产量与海水浓度的数据如下表:
(吨)的影响,通过在试验田的种植实验,测得了某种还水稻的亩产量与海水浓度的数据如下表:
海水浓度 |
|
|
|
|
|
亩产量 |
|
|
|
|
|
绘制散点图发现,可用线性回归模型拟合亩产量![]() 与海水浓度
与海水浓度![]() 之间的相关关系,用最小二乘法计算得
之间的相关关系,用最小二乘法计算得![]() 与
与![]() 之间的线性回归方程为
之间的线性回归方程为![]() .
.
(1)求出![]() 的值,并估算当浇灌海水浓度为8%时该品种的亩产量。
的值,并估算当浇灌海水浓度为8%时该品种的亩产量。
(2)①完成下列残差表:
海水浓度 |
|
|
|
|
|
亩产量 |
|
|
|
|
|
| |||||
残差 |
②统计学中常用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 越大,模型拟合效果越好,如假设
越大,模型拟合效果越好,如假设![]() ,就说明预报变量
,就说明预报变量![]() 的差异有
的差异有![]() 是由解释变量
是由解释变量![]() 引起的.请计算相关指数
引起的.请计算相关指数![]() (精确到0.01),并指出亩产量的变化多大程度上是由浇灌海水浓度引起的.
(精确到0.01),并指出亩产量的变化多大程度上是由浇灌海水浓度引起的.
(附:残差公式![]() ,相关指数
,相关指数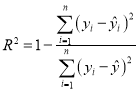 ,参考数据
,参考数据![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,
中,![]() 是过定点
是过定点![]() 且倾斜角为
且倾斜角为![]() 的直线;在极坐标系(以坐标原点
的直线;在极坐标系(以坐标原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴,取相同单位长度)中,曲线
轴非负半轴为极轴,取相同单位长度)中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的参数方程,并将曲线
的参数方程,并将曲线![]() 的方程化为直角坐标方程;
的方程化为直角坐标方程;
(2)若曲线![]() 与直线
与直线![]() 相交于不同的两点
相交于不同的两点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,如图4①,②,③,④为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
(1)求出f(5)的值;
(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你得到的关系式求出f(n)的表达式;
(3)求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com