
【题目】已知圆![]() :
:![]() ,椭圆
,椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,圆
,圆![]() 上任意一点
上任意一点![]() 处的切线交椭圆
处的切线交椭圆![]() 于两点
于两点![]() ,
,![]() ,当
,当![]() 恰好位于
恰好位于![]() 轴上时,
轴上时,![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)试判断![]() 是否为定值?若为定值,求出该定值;若不是定值,请说明理由.
是否为定值?若为定值,求出该定值;若不是定值,请说明理由.
【答案】(1)![]() (2)
(2)![]() 为定值且定值为
为定值且定值为![]() ,详见解析
,详见解析
【解析】
(1)根据题意,结合图形特点求解出![]() 与
与![]() 的长,再结合椭圆的离心率特点代换出关于
的长,再结合椭圆的离心率特点代换出关于![]() 的椭圆标准方程,将点
的椭圆标准方程,将点![]() 坐标代入椭圆方程即可求得标准方程
坐标代入椭圆方程即可求得标准方程
(2)分两种情况进行讨论,当过点![]() 的圆的切线斜率为0或不存在时,
的圆的切线斜率为0或不存在时,![]() ,当斜率存在时,设切线方程为
,当斜率存在时,设切线方程为![]() ,采用解析几何方法联立切线与椭圆标准方程,得出关于两点横坐标的韦达定理,再用弦长公式表示出
,采用解析几何方法联立切线与椭圆标准方程,得出关于两点横坐标的韦达定理,再用弦长公式表示出![]() ,最终将表达式进行化简求值即可
,最终将表达式进行化简求值即可
解:(1)由椭圆的离心率为![]() 知
知![]() 得
得![]() ,
,
∴椭圆![]() 的方程为
的方程为![]() .
.
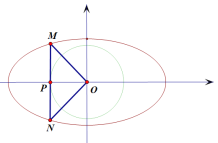
由圆的切线性质、圆的对称性及![]() 的面积为
的面积为![]() 得:
得:![]() ,
,
又![]() ,∴
,∴![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,将其代入椭圆方程得
,将其代入椭圆方程得![]() ,
,![]() ,
,
∴椭圆![]() 的方程为
的方程为![]() .
.
(2)①当过点![]() 的圆的切线斜率为0或不存在时,
的圆的切线斜率为0或不存在时,![]() ,
,
②当过点![]() 的圆的切线斜率存在且不为0时,设切线的方程为
的圆的切线斜率存在且不为0时,设切线的方程为![]() ,
,
![]() ,
,![]() ,∴
,∴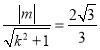 ,即
,即![]() .
.
联立直线和椭圆的方程得:![]() ,即
,即![]() ,
,
则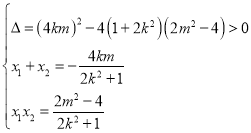 ,
,
设![]() ,则
,则
![]()
![]() ,
,
由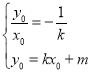 ,解得
,解得![]() ,
,
∴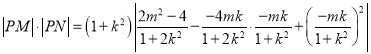
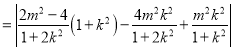
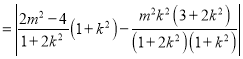
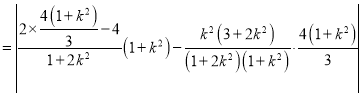
![]() ,
,
综上所述,![]() 为定值且定值为
为定值且定值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某企业有甲、乙两套设备生产同一种产品,为了检测两套设备的生产质量情况,随机从两套设备生产的大量产品中各抽取了50件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内,则为合格品,否则为不合格品. 表1是甲套设备的样本的频数分布表,图1是乙套设备的样本的频率分布直方图.
内,则为合格品,否则为不合格品. 表1是甲套设备的样本的频数分布表,图1是乙套设备的样本的频率分布直方图.
表1:甲套设备的样本的频数分布表
质量指标值 |
|
|
|
|
|
|
频数 | 1 | 5 | 18 | 19 | 6 | 1 |
图1:乙套设备的样本的频率分布直方图
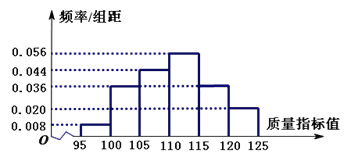
(1)将频率视为概率. 若乙套设备生产了5000件产品,则其中的不合格品约有多少件;
(2)填写下面列联表,并根据列联表判断是否有90%的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关;
甲套设备 | 乙套设备 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
| 0.15 | 0.10 | 0.050 |
| 2.072 | 2.706 | 3.841 |
附: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游胜地欲开发一座景观山,从山的侧面进行勘测,迎面山坡线![]() 由同一平面的两段抛物线组成,其中
由同一平面的两段抛物线组成,其中![]() 所在的抛物线以
所在的抛物线以![]() 为顶点、开口向下,
为顶点、开口向下,![]() 所在的抛物线以
所在的抛物线以![]() 为顶点、开口向上,以过山脚(点
为顶点、开口向上,以过山脚(点![]() )的水平线为
)的水平线为![]() 轴,过山顶(点
轴,过山顶(点![]() )的铅垂线为
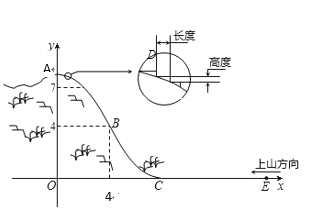
)的铅垂线为![]() 轴建立平面直角坐标系如图(单位:百米).已知
轴建立平面直角坐标系如图(单位:百米).已知![]() 所在抛物线的解析式
所在抛物线的解析式![]() ,
,![]() 所在抛物线的解析式为
所在抛物线的解析式为![]()
(1)求![]() 值,并写出山坡线
值,并写出山坡线![]() 的函数解析式;
的函数解析式;
(2)在山坡上的700米高度(点![]() )处恰好有一小块平地,可以用来建造索道站,索道的起点选择在山脚水平线上的点
)处恰好有一小块平地,可以用来建造索道站,索道的起点选择在山脚水平线上的点![]() 处,
处,![]() (米),假设索道
(米),假设索道![]() 可近似地看成一段以
可近似地看成一段以![]() 为顶点、开口向上的抛物线
为顶点、开口向上的抛物线![]() 当索道在
当索道在![]() 上方时,索道的悬空高度有最大值,试求索道的最大悬空高度;
上方时,索道的悬空高度有最大值,试求索道的最大悬空高度;
(3)为了便于旅游观景,拟从山顶开始、沿迎面山坡往山下铺设观景台阶,台阶每级的高度为20厘米,长度因坡度的大小而定,但不得少于20厘米,每级台阶的两端点在坡面上(见图).试求出前三级台阶的长度(精确到厘米),并判断这种台阶能否一直铺到山脚,简述理由?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 为两个不同的平面,
为两个不同的平面,![]() ,
,![]() 为两条不同的直线,有以下命题:
为两条不同的直线,有以下命题:
①若![]() ,
,![]() ,则
,则![]() .②若
.②若![]() ,
,![]() ,则
,则![]() .③若
.③若![]() ,
,![]() ,则
,则![]() .④若
.④若![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
其中真命题有()
A.①②B.①③C.②③D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为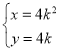 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 和曲线
和曲线![]() 的普通方程;
的普通方程;
(2)已知点![]() ,且直线
,且直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面给出了关于复数的四种类比推理:
①复数的加减法运算可以类比多项式的加减法运算法则;
②由向量![]() 的性质
的性质![]() ,类比得到复数
,类比得到复数![]() 的性质
的性质![]() ;
;
③方程![]() 有两个不同实数根的条件是
有两个不同实数根的条件是![]() 可以类比得到:方程
可以类比得到:方程![]() 有两个不同复数根的条件是
有两个不同复数根的条件是![]() ;
;
④由向量加法的几何意义可以类比得到复数加法的几何意义,其中类比错误的是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com