
【题目】梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于
于![]() (如图1).现沿
(如图1).现沿![]() 将
将![]() 折起,使得
折起,使得![]() ,得四棱锥
,得四棱锥![]() (如图2).
(如图2).
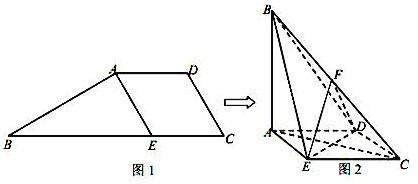
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 为
为![]() 的中点,求二面角
的中点,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析 (2)![]()
【解析】
(1)在![]() 中,求解三角形可得
中,求解三角形可得![]() ,又
,又![]() ,得到四边形
,得到四边形![]() 为平行四边形,进一步得到平行四边形
为平行四边形,进一步得到平行四边形![]() 为菱形,则
为菱形,则![]() ,再由
,再由![]() ,得
,得![]() 平面
平面![]() ,从而得到平面
,从而得到平面![]() 平面
平面![]() ;
;
(2)由![]() 平面
平面![]() ,得到
,得到![]() ,再由
,再由![]() ,得
,得![]() 平面
平面![]() ,设
,设![]() ,可得
,可得![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,则
的中点,则![]() ,得到
,得到![]() 平面
平面![]() ,以
,以![]() 为原点建立空间直角坐标系,分别求出平面
为原点建立空间直角坐标系,分别求出平面![]() 与平面
与平面![]() 的一个法向量,由两法向量所成角的余弦值可得二面角
的一个法向量,由两法向量所成角的余弦值可得二面角![]() 的余弦值.
的余弦值.
解:(1)在![]() 中,∵
中,∵![]() ,
,![]() ,∴
,∴![]() ,又
,又![]() ,∴
,∴![]() ,
,
又![]() ,∴四边形
,∴四边形![]() 为平行四边形.
为平行四边形.
∵![]() ,∴平行四边形
,∴平行四边形![]() 为菱形,∴
为菱形,∴![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
∴![]() 平面
平面![]() .
.
又∵![]()
![]() 平面
平面![]() ,∴.平面
,∴.平面![]() 平面
平面![]() .
.
(2)∵![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ,∴
,∴![]() ,
,
又![]() ,
,![]()
![]() 平面
平面![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() ,
,
设![]() ,∵
,∵![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,∴
的中点,∴![]() ,∴
,∴![]() 平面
平面![]() ,
,
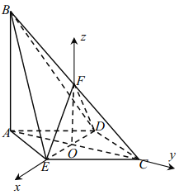
由(Ⅰ)得,以![]() 为原点,建立如图空间直角坐标系
为原点,建立如图空间直角坐标系![]() .
.
不妨设![]() ,可知
,可知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则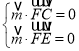 ,∴
,∴ ,
,
令![]() ,则
,则![]() ,
,![]() ,∴
,∴![]() ,
,
易得平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,则
,则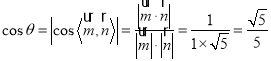 ,
,
即二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】边长为2正方体![]() 中,点E在棱CD上.
中,点E在棱CD上.
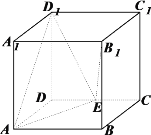
(1)求证:![]() ;
;
(2)若E是CD中点,求![]() 与平面
与平面![]() 所成的角的正弦值;
所成的角的正弦值;
(3)设M在棱![]() 上,且
上,且![]() ,是否存在点E,使平面
,是否存在点E,使平面![]() ⊥平面
⊥平面![]() ,若存在,指出点E的位置,若不存在,请说明理由.
,若存在,指出点E的位置,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一批产品共10件,其中3件是不合格品,用下列两种不同方式从中随机抽取2件产品检验:
方法一:一次性随机抽取2件;
方法二:先随机抽取1件,放回后再随机抽取1件.
记方法一抽取的不合格产品数为![]() .记方法二抽取的不合格产品数为
.记方法二抽取的不合格产品数为![]() .
.
(1)求两种抽取方式下![]() ,
,![]() 的概率分布列;
的概率分布列;
(2)比较两种抽取方式抽到的不合格品平均数的大小?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个结论中正确的个数是
(1)对于命题![]() 使得
使得![]() ,则
,则![]() 都有
都有![]() ;
;
(2)已知![]() ,则
,则 ![]()
(3)已知回归直线的斜率的估计值是2,样本点的中心为(4,5),则回归直线方程为![]() ;
;
(4)“![]() ”是“
”是“![]() ”的充分不必要条件.
”的充分不必要条件.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年春节期间,某超市准备举办一次有奖促销活动,若顾客一次消费达到400元则可参加一次抽奖活动,超市设计了两种抽奖方案.
方案一:一个不透明的盒子中装有30个质地均匀且大小相同的小球,其中10个红球,20个白球,搅拌均匀后,顾客从中随机抽取一个球,若抽到红球则顾客获得60元的返金券,若抽到白球则获得20元的返金券,且顾客有放回地抽取3次.
方案二:一个不透明的盒子中装有30个质地均匀且大小相同的小球,其中10个红球,20个白球,搅拌均匀后,顾客从中随机抽取一个球,若抽到红球则顾客获得80元的返金券,若抽到白球则未中奖,且顾客有放回地抽取3次.
(1)现有两位顾客均获得抽奖机会,且都按方案一抽奖,试求这两位顾客均获得180元返金券的概率;
(2)若某顾客获得抽奖机会.
①试分别计算他选择两种抽奖方案最终获得返金券的数学期望;
②为了吸引顾客消费,让顾客获得更多金额的返金券,该超市应选择哪一种抽奖方案进行促销活动?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com