
【题目】如图,四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点,
上一点,![]() ,
,![]() 为
为![]() 的中点.
的中点.
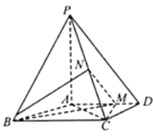
(1)证明:![]() 平面
平面![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离;
的距离;
(3)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析(2)![]() (3)
(3)![]()
【解析】
(1)取![]() 中点
中点![]() ,连接
,连接![]() ,根据已知条件,可证四边形
,根据已知条件,可证四边形![]() 为平行四边形,即可得证结论;
为平行四边形,即可得证结论;
(2)点![]() 到平面
到平面![]() 的距离,即为点
的距离,即为点![]() 到平面
到平面![]() 的距离,求出
的距离,求出![]() ,
,![]() 的面积,
的面积,![]() 等体积法,即可求出结论;
等体积法,即可求出结论;
(3)由(2)的结论,得出直线与平面所成的角,解直角三角形,即可求解.
(1)证明:取![]() 中点
中点![]() ,连接
,连接![]() ,
,
∵![]() 为
为![]() 的中点,∴
的中点,∴![]() ,且
,且![]() ,
,
又![]() ,且
,且![]() ,
,
∴![]() ,且
,且![]() ,
,
则![]() ,且
,且![]() ,
,
∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]() .
.
又∵![]() 平面
平面![]() .
.![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,∵
,∵![]() ,
,
∴![]() 且
且![]() ,∴四边形
,∴四边形![]() 是矩形,
是矩形,
∴![]() ,又∵
,又∵![]() 平面
平面![]() ,∴
,∴![]() ,
,
∴![]() 平面
平面![]() 且
且![]() ,
,
过点![]() 作
作![]() 平面
平面![]() 于
于![]() ,
,
则![]() 即为点
即为点![]() 到平面
到平面![]() 的距离.
的距离.
∵![]() ,∴
,∴![]() ,
,
![]() ,∴
,∴![]() .
.
(3)连接![]() 由(2)知
由(2)知
![]() 即为直线
即为直线![]() 与平面
与平面![]() 所成的角,
所成的角,
在![]() 中,
中,![]() ,
,![]() ,∴
,∴![]() ,
,
又∵![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.



 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
【题目】2018年国际乒联总决赛在韩国仁川举行,比赛时间为12月13﹣12月16日,在男子单打项目,中国队准备选派4人参加.已知国家一线队共6名队员,二线队共4名队员.
(1)求恰好有3名国家一线队队员参加比赛的概率;
(2)设随机变量![]() 表示参加比赛的国家二线队队员的人数,求
表示参加比赛的国家二线队队员的人数,求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C: ![]() ,直线l过点
,直线l过点![]() .
.

(1)若直线l与圆心C的距离为1,求直线l的方程;
(2)若直线l与圆C交于M,N两点,且![]() ,求以MN为直径的圆的方程;
,求以MN为直径的圆的方程;
(3)设直线![]() 与圆C交于A,B两点,是否存在实数a,使得直线l垂直平分弦AB?若存在,求出实数a的值;若不存在,说明理由.
与圆C交于A,B两点,是否存在实数a,使得直线l垂直平分弦AB?若存在,求出实数a的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若在定义域内存在实数x,满足
,若在定义域内存在实数x,满足![]() ,其中k为整数,则称函数
,其中k为整数,则称函数![]() 为定义域上的“k阶局部奇函数”.
为定义域上的“k阶局部奇函数”.
(1)已知函数![]() ,试判断
,试判断![]() 是否为
是否为![]() 上的“2阶局部奇函数”?并说明理由;
上的“2阶局部奇函数”?并说明理由;
(2)若![]() 是
是![]() 上的“1阶局部奇函数”,求实数m的取值范围;
上的“1阶局部奇函数”,求实数m的取值范围;
(3)若![]() ,对任意的实数
,对任意的实数![]() ,函数
,函数![]() 恒为
恒为![]() 上的“k阶局部奇函数”,求整数k取值的集合.
上的“k阶局部奇函数”,求整数k取值的集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体![]() 的棱长为
的棱长为![]() ,点E,F,G分别为棱AB,
,点E,F,G分别为棱AB,![]() ,
,![]() 的中点,下列结论中,正确结论的序号是___________.
的中点,下列结论中,正确结论的序号是___________.
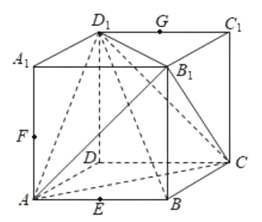
①过E,F,G三点作正方体的截面,所得截面为正六边形;
②![]() 平面EFG;
平面EFG;
③![]() 平面
平面![]() ;
;
④异面直线EF与![]() 所成角的正切值为
所成角的正切值为![]() ;
;
⑤四面体![]() 的体积等于
的体积等于![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com