练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某二手交易市场对某型号的二手汽车的使用年数（）与销售价格（单位：万元/辆）进行整理，得到如下的对应数据：

    使用年数

    2

    4

    6

    8

    10

    销售价格

    16

    13

    9.5

    7

    4.5

    （I）试求关于的回归直线方程.

    （参考公式：，）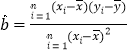

    （II）已知每辆该型号汽车的收购价格为万元，根据（I）中所求的回归方程，预测为何值时，销售一辆该型号汽车所获得的利润最大？（利润=销售价格-收购价格）

    【答案】（I）.

    （II）当时，利润取得最大值.

    【解析】分析：（I）由题意可求得，结合所给公式可得，从而可得线性回归方程．（II）由题意可得，根据二次函数的知识求得最值即可．

    详解：（I）由表中数据得

    ，

    ，

    ，

    ，

    ∴，

    ∴，

    ∴关于的回归直线方程为．

    （II）根据题意得利润

    ∴当时，利润取得最大值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】据悉,2017年教育机器人全球市场规模已达到8.19亿美元,中国占据全球市场份额10.8%.通过简单随机抽样得到40家中国机器人制造企业,下图是40家企业机器人的产值频率分布直方图.

    （1）求的值；

    （2）在上述抽取的40个企业中任取3个，抽到产值小于500万元的企业不超过两个的概率是多少？

    （3）在上述抽取的40个企业中任取2个,设为产值不超过500万元的企业个数减去超过500万元的企业个数的差值,求的分布列及期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝2x，x∈R.

    (1)当m取何值时，方程|f(x)－2|＝m有一个解？两个解？

    (2)若不等式[f(x)]2＋f(x)－m>0在R上恒成立，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某企业响应省政府号召，对现有设备进行改造，为了分析设备改造前后的效果，现从设备改造前后生产的大量产品中各抽取了件产品作为样本，检测一项质量指标值，若该项质量指标值落在内的产品视为合格品，否则为不合格品.如图是设备改造前的样本的频率分布直方图，表是设备改造后的样本的频数分布表.

    表：设备改造后样本的频数分布表

    质量指标值

    频数

    （1）完成下面的列联表，并判断是否有的把握认为该企业生产的这种产品的质量指标值与设备改造有关；

    设备改造前

    设备改造后

    合计

    合格品

    不合格品

    合计

    （2）根据频率分布直方图和表 提供的数据，试从产品合格率的角度对改造前后设备的优劣进行比较；

    （3）企业将不合格品全部销毁后，根据客户需求对合格品进行登记细分，质量指标值落在内的定为一等品，每件售价元；质量指标值落在或内的定为二等品，每件售价元；其它的合格品定为三等品，每件售价元.根据表的数据，用该组样本中一等品、二等品、三等品各自在合格品中的频率代替从所有产品中抽到一件相应等级产品的概率.现有一名顾客随机购买两件产品，设其支付的费用为（单位：元），求的分布列和数学期望.

    附：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（多选题）对任意实数,,,下列命题中正确的是（ ）

    A.“”是“”的充要条件

    B.“是无理数”是“是无理数”的充要条件

    C.“”是“”的充分条件

    D.“”是“”的必要条件

    E.“”是“”的必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出下列四个结论：

    ①从1，2，3，4，5中任取2个不同的数，事件“取到的2个数之和为偶数”，事件“取到的

    2个数均为偶数”，则；

    ②某班共有45名学生，其中30名男同学，15名女同学，老师随机抽查了5名同学的作业，用表示抽查到的女生的人数，则；

    ③设随机变量服从正态分布，，则；

    ④由直线，，曲线及轴所围成的图形的面积是.

    其中所有正确结论的序号为__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四边形ABCD外接于圆，AC是圆周角∠BAD的角平分线，过点C的切线与AD延长线交于点E，AC交BD于点F．

    （1）求证：BD∥CE；
    （2）若AB是圆的直径，AB=4，DE=1，求AD的长度．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系内，点实施变换后，对应点为，给出以下命题：

    ①圆上任意一点实施变换后，对应点的轨迹仍是圆；

    ②若直线上每一点实施变换后，对应点的轨迹方程仍是则；

    ③椭圆上每一点实施变换后，对应点的轨迹仍是离心率不变的椭圆；

    ④曲线上每一点实施变换后，对应点的轨迹是曲线，是曲线上的任意一点，是曲线上的任意一点，则的最小值为.

    以上正确命题的序号是___________________（写出全部正确命题的序号）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于函数，若，则称为的“不动点”，若，则称为的“稳定点”，函数的“不动点”和“稳定点”的集合分别记为和，即，，那么，

    （1）求函数的“稳定点”；

    （2）求证：；

    （3）若，且，求实数的取值范围.

    查看答案和解析>>

    同步练习册答案