
【题目】已知函数![]() (
(![]() ,且
,且![]() )在
)在![]() 上单调递增,且关于
上单调递增,且关于![]() 的方程
的方程![]() 恰有两个不相等的实数解,则
恰有两个不相等的实数解,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
由题意首先求得a的取值范围,然后结合函数的解析式将原问题转化为两函数图像存在两个交点的问题,数形结合即可确定a的取值范围.
由函数的解析式可知函数在区间![]() 上单调递增,
上单调递增,
当![]() 时,函数
时,函数![]() 单调递减,由复合函数的单调性法则可知:
单调递减,由复合函数的单调性法则可知:![]() ,
,
且函数在![]() 处满足:
处满足:![]() ,解得:
,解得:![]() ,故
,故![]() ,
,
方程![]() 恰有两个不相等的实数解,则函数
恰有两个不相等的实数解,则函数![]() 与函数
与函数![]() 的图像有且仅有两个不同的交点,
的图像有且仅有两个不同的交点,
绘制函数![]() 的图像如图中虚线所示,
的图像如图中虚线所示,
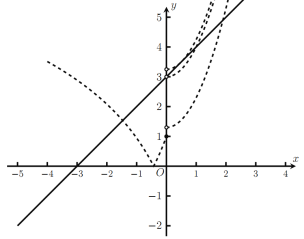
令![]() 可得:
可得:![]() ,
,
由![]() 可知
可知![]() ,
,![]() ,
,
则直线![]() 与函数
与函数![]() 的图像在区间
的图像在区间![]() 上存在唯一的交点,
上存在唯一的交点,
原问题转化为函数![]() 与二次函数
与二次函数![]() 在区间
在区间![]() 上存在唯一的交点,
上存在唯一的交点,
很明显当![]() ,即
,即![]() 时满足题意,
时满足题意,
当直线与二次函数相切时,设切点坐标为![]() ,亦即
,亦即![]() ,
,
由函数的解析式可得:![]() ,故:
,故:![]() ,则
,则![]() ,
,
切点坐标为![]() ,从而:
,从而:![]() ,即
,即![]() .
.
据此可得:![]() 的取值范围是
的取值范围是![]() .
.
故选:D.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】点![]() 、
、![]() 、
、![]() 分别是正方体
分别是正方体![]() 的棱
的棱![]() ,
,![]() ,
,![]() 的中点,则下列命题中的真命题是__________(写出所有真命题的序号).
的中点,则下列命题中的真命题是__________(写出所有真命题的序号).
①以正方体的顶点为顶点的三棱锥的四个面中最多可以四个面都是直角三角形;
②点![]() 在直线
在直线![]() 上运动时,总有
上运动时,总有![]() ;
;
③点![]() 在直线
在直线![]() 上运动时,三棱锥
上运动时,三棱锥![]() 的体积是定值;
的体积是定值;
④若![]() 是正方体的面
是正方体的面![]() ,(含边界)内一动点,且点
,(含边界)内一动点,且点![]() 到点
到点![]() 和
和![]() 的距离相等,则点
的距离相等,则点![]() 的轨迹是一条线段.
的轨迹是一条线段.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】C反应蛋白(CRP)是机体受到微生物入侵或组织损伤等炎症性刺激时细胞合成的急性相蛋白,医学认为CRP值介于0-10mg/L为正常值.下面是某患者在治疗期间连续5天的检验报告单中CRP值(单位:mg/L)与治疗大数的统计数据:
治疗天数x | 1 | 2 | 3 | 4 | 5 |
CRP值y | 51 | 40 | 35 | 28 | 21 |
(1)若CRP值y与治疗数x只有线性相关关系试用最小乘法求出y关于x的线性回归方程,并估计该者至少需要治疗多少天CRP值可以回到正常水平;
(2)为均衡城乡保障待遇,统一保障范同和支付准,为多保人员提供公平的基本医疗保障.某市城乡医疗保险实施办法指出:门诊报销比例为50%;住院报销比例,A类医疗机构80%,B类医疗机构60%.若张华参加了城乡基本医疗保险,他因CRP偏高选择在医疗机构治疗,医生为张华提供了三种治疗方案:方案一:门诊治疗,预计每天诊疗费80元;方案二:住院治疗,A类医疗机构,入院检查需花费600元,预计每天诊疗费100元;方案三:住院治疗,B类医疗机构,入院检查需花费400元,预计每天诊疗费40元;若张华需要经过连续治疗n天![]() ,请你为张华选择最经济实惠的治疗方案.
,请你为张华选择最经济实惠的治疗方案.
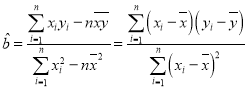 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】C反应蛋白(CRP)是机体受到微生物入侵或组织损伤等炎症性刺激时肝细胞合成的急性相蛋白,医学认为CRP值介于0-10mg/L为正常值下面是某患者在治疗期间连续5天的检验报告单中CRP值(单位:mg/L)与治疗天数的统计数据:
治疗天数x | 1 | 2 | 3 | 4 | 5 |
CRP值y | 51 | 40 | 35 | 28 | 21 |
(1)若CRP值y与治疗天数x具有线性相关关系,试用最小二乘法求出y关于x的线性回归方程,并估计该患者至少需要治疗多少天CRP值可以到正常水平;
(2)为均衡城乡保障待遇,统一保障范围和支付标准,为参保人员提供公平的基本医疗保障.某市城乡医疗保险实施办法指出:门诊报销比例为50%:住院报销比例,A类医疗机构80%,B类医疗机构60%.若张华参加了城乡基本医疗保险,他因CRP偏高选择在某医疗机构治疗,医生为张华提供了三种治疗方案:
方案一:门诊治疗,预计每天诊疗费80元;
方案二:住院治疗,A类医疗机构,入院检查需花费600元,预计每天诊疗费100元;
方案三:住院治疗,B类医疗机构,入院检查需花费400元,预计每天诊疗费40元;
若张华需要经过连续治疗n天,![]() ,请你为张华选择最经济实惠的治疗方案.
,请你为张华选择最经济实惠的治疗方案.
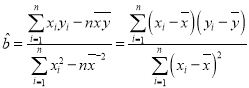 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列五个命题:
①“![]() ”是“
”是“![]() 为R上的增函数”的充分不必要条件;
为R上的增函数”的充分不必要条件;
②函数![]() 有两个零点;
有两个零点;
③集合A={2,3},B={1,2,3},从A,B中各任意取一个数,则这两数之和等于4的概率是![]() ;
;
④动圆C即与定圆![]() 相外切,又与y轴相切,则圆心C的轨迹方程是
相外切,又与y轴相切,则圆心C的轨迹方程是![]()
⑤若对任意的正数x,不等式![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是
的取值范围是![]()
其中正确的命题序号是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是衡量空气污染程度的一个指标,为了了解
是衡量空气污染程度的一个指标,为了了解![]() 市空气质量情况,从
市空气质量情况,从![]() 年每天的
年每天的![]() 值的数据中随机抽取
值的数据中随机抽取![]() 天的数据,其频率分布直方图如图所示.将
天的数据,其频率分布直方图如图所示.将![]() 值划分成区间
值划分成区间![]() 、
、![]() 、
、![]() 、
、![]() ,分别称为一级、二级、三级和四级,统计时用频率估计概率 .
,分别称为一级、二级、三级和四级,统计时用频率估计概率 .

(1)根据![]() 年的数据估计该市在
年的数据估计该市在![]() 年中空气质量为一级的天数;
年中空气质量为一级的天数;
(2)如果![]() 市对环境进行治理,经治理后,每天
市对环境进行治理,经治理后,每天![]() 值
值![]() 近似满足正态分布
近似满足正态分布![]() ,求经过治理后的
,求经过治理后的![]() 值的均值下降率.
值的均值下降率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】画糖是一种以糖为材料在石板上进行造型的民间艺术,常见于公园与旅游景点.某师傅制作了一种新造型糖画,为了进行合理定价先进性试销售,其单价![]() (元)与销量
(元)与销量![]() (个)相关数据如下表:
(个)相关数据如下表:

(1)已知销量![]() 与单价
与单价![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性相关方程;
的线性相关方程;
(2)若该新造型糖画每个的成本为![]() 元,要使得进入售卖时利润最大,请利用所求的线性相关关系确定单价应该定为多少元?(结果保留到整数)
元,要使得进入售卖时利润最大,请利用所求的线性相关关系确定单价应该定为多少元?(结果保留到整数)
参考公式:线性回归方程![]() 中斜率和截距最小二乘法估计计算公式:
中斜率和截距最小二乘法估计计算公式:

![]() .参考数据:
.参考数据:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com