
【题目】设![]() ,若函数
,若函数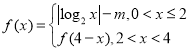 有4个不同的零点
有4个不同的零点![]() ,且
,且![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
先求出函数的解析式,根据题意,由零点,可以得方程,然后常变量分离,构造函数,利用新构造函数的对称性,得到![]() 之间的关系,再根据对数的运算性质,得到
之间的关系,再根据对数的运算性质,得到![]() 之间的关系,这样可以把
之间的关系,这样可以把![]() 化简成关于
化简成关于![]() 的代数式,最后利用换元法,基本不等式以及函数的单调性求出值域即可.
的代数式,最后利用换元法,基本不等式以及函数的单调性求出值域即可.
当![]() 时,所以有
时,所以有![]() ,因此有
,因此有![]() ,所以函数的解析式为:
,所以函数的解析式为: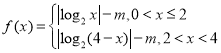 ,由题意可知:
,由题意可知:![]() 有四个不同的实数解,因此有:
有四个不同的实数解,因此有: ,设函数
,设函数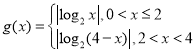 ,因此由可知:函数
,因此由可知:函数![]() 的图象与函数
的图象与函数![]() 的图象有四个不同的交点,函数
的图象有四个不同的交点,函数![]() 的图象如下图所示:
的图象如下图所示:
要想函数![]() 的图象与函数
的图象与函数![]() 的图象有四个不同的交点,必须有
的图象有四个不同的交点,必须有![]() ,此时有
,此时有![]() ,再由
,再由![]() ,结合图象可知:
,结合图象可知:![]() 函数是关于直线
函数是关于直线![]() 对称,因此有
对称,因此有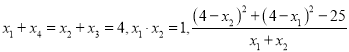
![]() ,所以
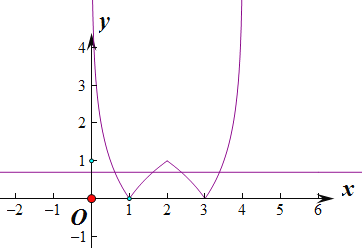
,所以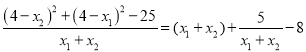 ,令
,令![]() ,令
,令![]() ,显然函数在
,显然函数在![]() 上单调递减,
上单调递减,
在![]() 上单调递增,
上单调递增,
故![]() ,
,![]() .
.
故选:A


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:
【题目】改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
支付方式 | (0,1000] | (1000,2000] | 大于2000 |
仅使用A | 18人 | 9人 | 3人 |
仅使用B | 10人 | 14人 | 1人 |
(Ⅰ)从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率;
(Ⅱ)从样本仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金额大于1000元的人数,求X的分布列和数学期望;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A的学生中,随机抽查3人,发现他们本月的支付金额都大于2000元.根据抽查结果,能否认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的两个焦点分别为
的两个焦点分别为![]() 和
和![]() ,短轴的两个端点分别为
,短轴的两个端点分别为![]() 和
和![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且满足
上,且满足![]() ,当
,当![]() 变化时,给出下列三个命题:
变化时,给出下列三个命题:
①点![]() 的轨迹关于
的轨迹关于![]() 轴对称;②
轴对称;②![]() 的最小值为2;
的最小值为2;
③存在![]() 使得椭圆
使得椭圆![]() 上满足条件的点
上满足条件的点![]() 仅有两个,
仅有两个,
其中,所有正确命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1:![]() ,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C2是圆心极坐标为(3,π),半径为1的圆.
,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C2是圆心极坐标为(3,π),半径为1的圆.
(1)求曲线C1的参数方程和C2的直角坐标方程;
(2)设M,N分别为曲线C1,C2上的动点,求|MN|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱柱ABC﹣A1B1C1,平面A1ACC1⊥平面ABC,∠ABC=90°,∠BAC=30°,A1A=A1C=AC,E,F分别是AC,A1B1的中点.
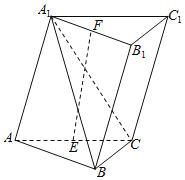
(1)证明:EF⊥BC;
(2)求直线EF与平面A1BC所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|+|x+2|.
(1)若a=1.解不等式f(x)≤x2﹣1;
(2)若a>0,b>0,c>0.且f(x)的最小值为4﹣b﹣c.求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅原理“幂势既同,则积不容异”中的“幂”指面积,“势”即是高,意思是:若两个等高的几何体在所有等高处的水平截面的面积恒等,则这两几何体的体积相等.设夹在两个平行平面之间的几何体的体积分别为![]() ,它们被平行于这两个平面的任意平面截得的两个截面面积分别为
,它们被平行于这两个平面的任意平面截得的两个截面面积分别为![]() ,则“
,则“![]() 恒成立”是“
恒成立”是“![]() ”的( )
”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com