Question

已知椭圆C:3x²+4y²=12,试确定m的取值范围,使得对于直线l:y=4x+m,椭圆C上有不同的两点关于这条直线对称.

Answer 1

思路分析:解此题的关键是构造不等式来求m的范围,一般采用判别式,或点与曲线的位置关系.

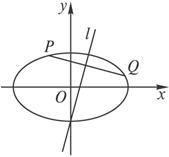
解法一:设椭圆C上关于直线l对称的两点为P(x₁,y₁)、Q(x₂,y₂),其所在直线方程为y=-x+b,代入椭圆方程3x²+4y²=12.

    整理得13x²-8bx+16b²-48=0,

∵x₁≠x₂,

∴Δ=-12(4b²-13)＞0.

解得-＜b＜.                                                         ①

又∵,

而点()又在直线y=4x+m上,

∴m=.                                            ②

把①代入②得m的取值范围是-＜m＜.

解法二:由解法一知2x₀=x₁+x₂=,x₁x₂=.

其中PQ的中点坐标为M(x₀,y₀),

由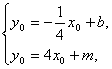

消去y₀,把x₀=b代入可解得m=-b,x₀=-m,

根据中点M的位置,必有(x₁-x₀)(x₂-x₀)＜0,即x₁x₂-x₀(x₁+x₂)+x₀²＜0.

由此解得-＜m＜.

解法三:设椭圆上关于l对称的两点为P(x₁,y₁)、Q(x₂,y₂),PQ的中点M(x₀,y₀).

则可求得.                                           ①

又点M在l上,

∴y₀=4x₀+m.                                                               ②

由①②联立解得x₀=-m,y₀=-3m.

∵M(-m,-3m)在椭圆的内部,

∴3(-m)²+4(-3m)²＜12,

解得-＜m＜.