
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 上一点,且
上一点,且![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,
,![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析(2)![]() .
.
【解析】
试题分析:(1)法一:过![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,由
,由![]() ,推出
,推出![]() ,结合
,结合![]() 与
与![]() ,即可推出四边形
,即可推出四边形![]() 为平行四边形,即可证明结论;法二:过点
为平行四边形,即可证明结论;法二:过点![]() 作
作![]() 于点
于点![]() ,
,![]() 为垂足,连接
为垂足,连接![]() ,由题意,
,由题意,![]() ,则
,则![]() ,即可推出四边形
,即可推出四边形![]() 为平行四边形,再由
为平行四边形,再由![]() 平面
平面![]() ,可推出
,可推出![]() ,即可得证平面
,即可得证平面![]() 平面
平面![]() ,从而得证结论;(2)过
,从而得证结论;(2)过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,结合
,结合![]() 平面
平面![]() ,可推出
,可推出![]() 平面
平面![]() ,由
,由![]() 平面
平面![]() ,可得
,可得![]() 到平面
到平面![]() 的距离等于
的距离等于![]() 到平面
到平面![]() 的距离,即
的距离,即![]() ,再根据
,再根据![]() ,
,![]() ,即可求出三棱锥
,即可求出三棱锥![]() 的体积.
的体积.
试题解析:(1)法一:过![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
∵![]()
∴![]() .
.
又∵![]() ,且
,且![]() ,
,
∴![]() ,∴四边形
,∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() .
.
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
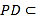
法二:过点![]() 作
作![]() 于点
于点![]() ,
,![]() 为垂足,连接
为垂足,连接![]() .
.
由题意,![]() ,则
,则![]() ,
,
又∵![]() ,
,![]()
∴![]() ,
,
∴四边形![]() 为平行四边形
为平行四边形
∴![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]() .
.
又![]()
∴![]() .
.
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ;
;
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ;
;
∴平面![]() 平面
平面![]() .
.
∵![]() 平面
平面![]()
∴![]() 平面
平面![]() .
.
(2)过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]()
∴![]() .
.
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ;
;
∴![]() 平面
平面![]()
由(1)知,![]() 平面
平面![]() ,
,
所以![]() 到平面
到平面![]() 的距离等于
的距离等于![]() 到平面
到平面![]() 的距离,即
的距离,即![]() .
.
在![]() 中,
中,![]() ,
,![]()
∴![]() .
.
![]()
![]() .
.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,AC=BC=PC=2,AB=PA=PB=2![]() .
.
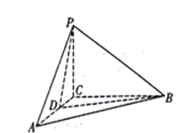
(1)证明:PC⊥平面ABC;
(2)若点D在棱AC上,且二面角D-PB-C为30°,求PD与平面PAB所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,A、B、C所对的边分别是a、b、c,且有bcosC+ccosB=2acosB.
(1)求B的大小;
(2)若△ABC的面积是![]() ,且a+c=5,求b.
,且a+c=5,求b.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象经过(-1,0)点,且在x=-1处的切线斜率为-1,设数列
的图象经过(-1,0)点,且在x=-1处的切线斜率为-1,设数列![]() 的前n项和Sn=f(n)(n∈N*).
的前n项和Sn=f(n)(n∈N*).
(1)求数列![]() 的通项公式;
的通项公式;
(2)求数列{![]() }前n项的和Tn.
}前n项的和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产的某种零件的尺寸![]() 大致服从正态分布
大致服从正态分布![]() ,且规定尺寸
,且规定尺寸![]() 为次品,其余的为正品.生产线上的打包机自动把每5件零件打包成1箱,然后进入销售环节,若每销售一件正品可获利50元,每销售一件次品亏损100元.现从生产线生产的零件中抽样20箱做质量分析,作出的频率分布直方图如下:
为次品,其余的为正品.生产线上的打包机自动把每5件零件打包成1箱,然后进入销售环节,若每销售一件正品可获利50元,每销售一件次品亏损100元.现从生产线生产的零件中抽样20箱做质量分析,作出的频率分布直方图如下:
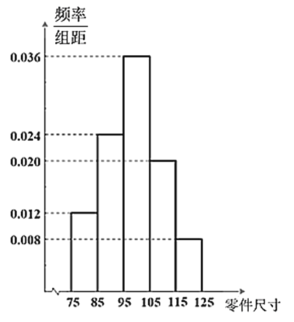
(1)估计生产线生产的零件的次品率及零件的平均尺寸;
(2)从生产线上随机取一箱零件,求这箱零件销售后的期望利润及不亏损的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某人在塔的正东方向上的![]() 处在与塔垂直的水平面内沿南偏西
处在与塔垂直的水平面内沿南偏西![]() 的方向以每小时
的方向以每小时![]() 千米的速度步行了
千米的速度步行了![]() 分钟以后,在点
分钟以后,在点![]() 处望见塔的底端
处望见塔的底端![]() 在东北方向上,已知沿途塔的仰角
在东北方向上,已知沿途塔的仰角![]() ,
,![]() 的最大值为
的最大值为![]() .
.
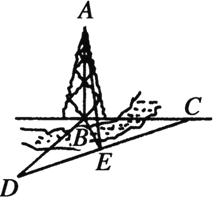
(1)求该人沿南偏西![]() 的方向走到仰角
的方向走到仰角![]() 最大时,走了几分钟;
最大时,走了几分钟;
(2)求塔的高![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知直线l过点![]() .
.
(1)若直线l的纵截距和横截距相等,求直线l的方程;
(2)若直线l与两坐标轴围成的三角形的面积为![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com