
【题目】设函数![]() ,
,![]() .
.
(1)若曲线![]() 与曲线
与曲线![]() 在它们的交点
在它们的交点![]() 处具有公共切线,求a,b的值;
处具有公共切线,求a,b的值;
(2)当![]() 时,若函数
时,若函数![]() 在区间
在区间![]() 内恰有两个零点,求a的取值范围;
内恰有两个零点,求a的取值范围;
(3)![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最小值.
上的最小值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)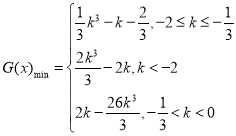
【解析】
(1)由题意求出![]() 由题意得
由题意得![]() ,且
,且![]() 解该方程组即可求出
解该方程组即可求出![]() 的值;(2)把
的值;(2)把![]() 代入
代入![]() 化简,并求出
化简,并求出![]() ,利用导数求出单调性和极值,由函数在
,利用导数求出单调性和极值,由函数在![]() 内有两零点列出不等式组,求出不等式的解集可得
内有两零点列出不等式组,求出不等式的解集可得![]() 的取值范围.
的取值范围.
(3)表示出![]() ,并求出
,并求出![]() ,利用导数求出单调性和极值点,按照在区间
,利用导数求出单调性和极值点,按照在区间![]() 内没有极值点,一个极值点,两个极值点分类讨论,结合图象及函数的单调性即可求得其最小值.
内没有极值点,一个极值点,两个极值点分类讨论,结合图象及函数的单调性即可求得其最小值.
(1)![]() ,
,![]() ,
,
![]() 由线
由线![]() 与曲线
与曲线![]() 在它们的交点
在它们的交点![]() 处具有公共切线,
处具有公共切线,
![]() ,
,![]() ,
,
即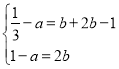 ,
,
解得![]() .
.
(2)![]() ,
,
![]() ,
,
![]()
![]() ,
,
令![]() ,得
,得![]() ,
,![]() ,
,
|
|
|
|
|
|
| |
|
| 极小值 |
|
![]() 在
在![]() 内恰有2个零点,
内恰有2个零点,
 ,即
,即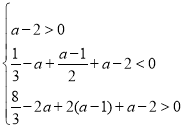 ,
,
解得![]() ,
,
因此a的取值范围是![]() .
.
(3)![]()
![]()
![]()
![]()
令![]() ,解得
,解得![]() ,
,
|
|
|
|
|
|
|
| 0 |
| 0 |
|
|
| 极大值 |
| 极小值 |
|
①当![]() ,即
,即![]() 时,
时,![]() ,
,
![]() 在
在![]() 和
和![]() 单调递增,
单调递增,
![]() 在
在![]() 上单调递减,
上单调递减,
![]() ,
,
![]()
![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() .
.
②![]() ,即
,即![]() ,
,
![]() 在
在![]() 上单调递减,
上单调递减,
![]() .
.
③![]() ,即
,即![]() ,
,
![]() 在
在![]() 上单调递减,
上单调递减,
![]() 在
在![]() 单调递增,
单调递增,
![]() .
.
综上所述,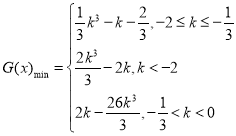 .
.


科目:高中数学 来源: 题型:
【题目】直线![]() ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为( ).
ax+by=1与圆x2+y2=1相交于A,B两点(其中a,b是实数),且△AOB是直角三角形(O是坐标原点),则点P(a,b)与点(0,1)之间距离的最小值为( ).
A.0B.![]() C.
C.![]() -1D.
-1D.![]() +1
+1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学根据学生的兴趣爱好,分别创建了“书法”、“诗词”、“理学”三个社团,据资料统计新生通过考核选拔进入这三个社团成功与否相互独立.2015年某新生入学,假设他通过考核选拔进入该校的“书法”、“诗词”、“理学”三个社团的概率依次为![]() 、
、![]() 、
、![]() ,己知三个社团他都能进入的概率为
,己知三个社团他都能进入的概率为![]() ,至少进入一个社团的概率为
,至少进入一个社团的概率为![]() ,且
,且![]() .
.
(1)求![]() 与
与![]() 的值;
的值;
(2)该校根据三个社团活动安排情况,对进入“书法”社的同学增加校本选修学分1分,对进入“诗词”社的同学增加校本选修学分2分,对进入“理学”社的同学增加校本选修学分3分.求该新同学在社团方面获得校本选修课学分分数不低于4分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 ,其中
,其中![]() 为参数,
为参数,![]() .在以坐标原点
.在以坐标原点![]() 为极点,轴的正半轴为极轴的极坐标系中,点
为极点,轴的正半轴为极轴的极坐标系中,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)若![]() 是曲线
是曲线![]() 上的动点,
上的动点,![]() 为线段
为线段![]() 的中点.求点
的中点.求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数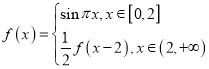 ,有下列说法:
,有下列说法:
①函数![]() 对任意
对任意![]() ,都有
,都有![]() 成立;
成立;
②函数![]() 在
在![]() 上单调递减;
上单调递减;
③函数![]() 在
在![]() 上有3个零点;
上有3个零点;
④若函数![]() 的值域为
的值域为![]() ,设
,设![]() 是
是![]() 中所有有理数的集合,若简分数
中所有有理数的集合,若简分数![]() (其中
(其中![]() ,
,![]() 为互质的整数),定义函数
为互质的整数),定义函数![]() ,则
,则![]() 在
在![]() 中根的个数为5;
中根的个数为5;
其中正确的序号是______(填写所有正确结论的番号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家举行大型的促销活动,经测算某产品当促销费用为![]() 万元时,销售量
万元时,销售量![]() 万件满足
万件满足![]() (其中
(其中![]() ,
, ![]() 为正常数),现假定生产量与销售量相等,已知生产该产品
为正常数),现假定生产量与销售量相等,已知生产该产品![]() 万件还需投入成本
万件还需投入成本![]() 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为![]() 万元/万件.
万元/万件.
(1)将该产品的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;
万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2013年华人数学家张益唐证明了孪生素数猜想的一个弱化形式。孪生素数猜想是希尔伯特在1900年提出的23个问题之一,可以这样描述:存在无穷多个素数p,使得p+2是素数,素数对(p,p+2)称为孪生素数.在不超过30的素数中,随机选取两个不同的数,其中能够组成孪生素数的概率是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 为梯形,
为梯形, ![]() ,且
,且![]() ,
, ![]() 是边长为2的正三角形,顶点
是边长为2的正三角形,顶点![]() 在
在![]() 上的射影为点
上的射影为点![]() ,且
,且![]() ,
, ![]() ,
, ![]() .
.
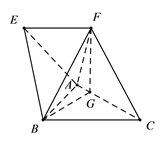
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com