【题目】已知函数f（x）=（sinx+cosx）2-cos2x.
（I）求f（x）的最小正周期；
（II）求证：当x∈[0， 
]时，f（x）≥0.
【答案】（I）
;（II）证明见解析.
【解析】试题分析：（I）根据三角恒等变换的公式，化简函数
，即求解函数的最小正周期；
（II）由（I）可知
的解析式，由题意求得
，得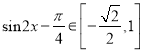
，即可求得函数的值域，从而做出证明.
试题解析：
（I）因为f（x）=sin2x+cos2x+sin2x-cos2x
=1+sin2x-cos2x=
sin（2x-
）+1.
所以函数f（x）的最小正周期为
.
（II）由（I）可知，f（x）=
sin（2x-
）+1.
当x
[0， 
]时，2x-
[-
， 
]，sin（2x-
）
[-
，1]，
sin（2x-
）+1∈[0， 
+l].
当2x-
=-
，即x=0时，f（x）取了最小值0.所以当x∈[0， 
]时，f（x）≥0.
名校课堂系列答案科目：高中数学 来源： 题型：
【题目】某中学高一女生共有450人，为了了解高一女生的身高情况，随机抽取部分高一女生测量身高，所得数据整理后列出频率分布表如下：
组别 | 频数 | 频率 |
145.5～149.5 | 8 | 0.16 |
149.5～153.5 | 6 | 0.12 |
153.5～157.5 | 14 | 0.28 |
157.5～161.5 | 10 | 0.20 |
161.5～165.5 | 8 | 0.16 |
165.5～169.5 |
|
|
合计 |
|
|
（1）求出表中字母
所对应的数值；
（2）在给出的直角坐标系中画出频率分布直方图；
（3）估计该校高一女生身高在149.5～165.5
范围内有多少人？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知定义在
上的函数
和数列
满足下列条件：
，
，当
且
时，
且
，其中
、
均为非零常数．
（1）若是等差数列，求实数的值；
（2）令
（），若
，求数列
的通项公式；
（3）令（），若
，数列
满足
，若数列有最大值
，最小值
，且
，求的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在三棱柱ABC-A1B1C1中，底面ABC为正三角形，侧棱AA1⊥底面ABC.已知D是BC的中点，AB=AA1=2.
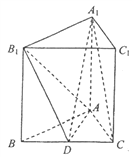
（I）求证：平面AB1D⊥平面BB1C1C；
（II）求证：A1C∥平面AB1D；
（III）求三棱锥A1-AB1D的体积.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在高中学习过程中，同学们经常这样说“如果物理成绩好，那么学习数学就没什么问题”某班针对“高中生物理对数学学习的影响”进行研究，得到了学生的物理成绩与数学成绩具有线性相关关系的结论，现从该班随机抽取5名学生在一次考试中的物理和数学成绩，如表：
编号成绩 | 1 | 2 | 3 | 4 | 5 |
物理(x) | 90 | 85 | 74 | 68 | 63 |
数学(y) | 130 | 125 | 110 | 95 | 90 |
(1)求数学y成绩关于物理成绩x的线性回归方程
(
精确到0.1)，若某位学生的物理成绩为80分时，预测他的数学成绩．
(2)要从抽取的这五位学生中随机选出三位参加一项知识竞赛，以x表示选中的学生的数学成绩高于100分的人数，求随机变量X的分布列及数学期望．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】(2016·山东卷)已知数列{an}的前n项和Sn＝3n2＋8n，{bn}是等差数列，且an＝bn＋bn＋1.
(1)求数列{bn}的通项公式；
(2)令cn＝
，求数列{cn}的前n项和Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
