
【题目】已知椭圆C: ![]() (a>b>0)过点(
(a>b>0)过点( ![]() ,1),且焦距为2
,1),且焦距为2 ![]() .
.
(1)求椭圆C的方程;
(2)若直线l:y=k(x+1)(k>﹣2)与椭圆C相交于不同的两点A、B,线段AB的中点M到直线2x+y+t=0的距离为 ![]() ,求t(t>2)的取值范围.
,求t(t>2)的取值范围.
【答案】
(1)解:由2c=2 ![]() ,c=
,c= ![]() ,则a2﹣b2=2,
,则a2﹣b2=2,
将点( ![]() ,1)代入椭圆方程:
,1)代入椭圆方程: ![]() ,解得:a2=4,b2=2,
,解得:a2=4,b2=2,
∴椭圆的标准方程: ![]()
(2)解:A(x1,y1),B(x2,y2),M(x0,y0)
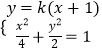 ,整理得:(2k2+1)x2+4k2x+2k2﹣4=0,
,整理得:(2k2+1)x2+4k2x+2k2﹣4=0,
则x1+x2=﹣ ![]() ,则x0=
,则x0= ![]() =﹣
=﹣ ![]() ,
,
y0=k(x0+1)= ![]() ,
,
由M到直线2x+y+t=0的距离 ![]() ,
, 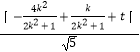 =
= ![]() ,
,
则丨 ![]() +t﹣2丨=3,
+t﹣2丨=3,
由k>﹣2及t>2,则t=5﹣ ![]() =5﹣
=5﹣ ![]() ,
,
由 ![]() ≥6
≥6 ![]() ,
,
∴5﹣ ![]() ≤t<5,即4﹣
≤t<5,即4﹣ ![]() ≤t<5,
≤t<5,
∴t(t>2)的取值范围[4﹣ ![]() ,5)
,5)
【解析】(1)由c= ![]() ,则a2﹣b2=2,将点代入椭圆方程,联立即可求得a和b的值,即可求得椭圆方程;(2)将直线方程代入椭圆方程,利用韦达定理及中点坐标公式求得M点坐标,利用点到直线的距离公式,根据k及t的取值范围,利用基本不等式的性质,即可求得t的取值范围.
,则a2﹣b2=2,将点代入椭圆方程,联立即可求得a和b的值,即可求得椭圆方程;(2)将直线方程代入椭圆方程,利用韦达定理及中点坐标公式求得M点坐标,利用点到直线的距离公式,根据k及t的取值范围,利用基本不等式的性质,即可求得t的取值范围.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C1的方程为 ![]() +
+ ![]() =1,双曲线C2的左、右焦点分别是C1的左、右顶点,而以双曲线C2的左、右顶点分别是椭圆C1的左、右焦点.
=1,双曲线C2的左、右焦点分别是C1的左、右顶点,而以双曲线C2的左、右顶点分别是椭圆C1的左、右焦点.
(1)求双曲线C2的方程;
(2)记O为坐标原点,过点Q(0,2)的直线l与双曲线C2相交于不同的两点E、F,若△OEF的面积为2 ![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆方程为 ![]() +y2=1,圆C:(x﹣1)2+y2=r2 .
+y2=1,圆C:(x﹣1)2+y2=r2 . 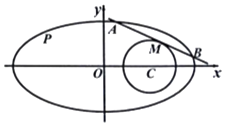
(Ⅰ)求椭圆上动点P与圆心C距离的最小值;
(Ⅱ)如图,直线l与椭圆相交于A、B两点,且与圆C相切于点M,若满足M为线段AB中点的直线l有4条,求半径r的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据微信同程旅游的调查统计显示,参与网上购票的1000位购票者的年龄(单位:岁)情况如图所示. 
(1)已知中间三个年龄段的网上购票人数成等差数列,求a,b的值;
(2)为鼓励大家网上购票,该平台常采用购票就发放酒店入住代金券的方法进行促销,具体做法如下:年龄在[30,50)岁的每人发放20元,其余年龄段的每人发放50元,先按发放代金券的金额采用分层抽样的方式从参与调查的1000位网上购票者中抽取5人,并在这5人中随机抽取3人进行回访调查,求此3人获得代金券的金额总和为90元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() mcos2x+(m﹣2)sinx,其中1≤m≤2,若函数f(x)的最大值记为g(m),则g(m)的最小值为( )
mcos2x+(m﹣2)sinx,其中1≤m≤2,若函数f(x)的最大值记为g(m),则g(m)的最小值为( )
A.﹣ ![]()
B.1
C.3﹣ ![]()
D.![]() ﹣1
﹣1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点E(﹣2,0),点P时圆F:(x﹣2)2+y2=36上任意一点,线段EP的垂直平分线交FP于点M,点M的轨迹记为曲线C.
(Ⅰ)求曲线C的方程;
(Ⅱ)过F的直线交曲线C于不同的A、B两点,交y轴于点N,已知 ![]() =m
=m ![]() ,
, ![]() =n
=n ![]() ,求m+n的值.
,求m+n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(单位:cm),则该阳马的外接球的体积为( ) 
A.100πcm3
B.![]()
C.400πcm3
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用数学归纳法证明1+2+3+…+n2= ![]() ,则当n=k+1时左端应在n=k的基础上加上( )
,则当n=k+1时左端应在n=k的基础上加上( )
A.k2+1
B.(k+1)2
C.![]()
D.(k2+1)+(k2+2)+(k2+3)+…+(k+1)2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com