
【题目】已知函数![]() 在
在![]() 上是奇函数.
上是奇函数.
(1)求![]() ;
;
(2)对![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)令![]() ,若关于
,若关于![]() 的方程
的方程![]() 有唯一实数解,求实数
有唯一实数解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]()
(2)![]()
(3)![]() 或
或![]()
【解析】试题分析:(1)函数![]() 是奇函数,所以
是奇函数,所以![]() ,解方程求a.(2)对于任意
,解方程求a.(2)对于任意![]() ,函数f(x)恒大于0,不等式
,函数f(x)恒大于0,不等式![]() 恒成立,即不等式
恒成立,即不等式![]() 恒成立,则
恒成立,则![]() 。(3)先求
。(3)先求![]() ,由
,由![]() 得g(2x)=mg(x+1)即
得g(2x)=mg(x+1)即![]() ,所以
,所以![]() (*),令
(*),令![]() ,则方程(*)变为
,则方程(*)变为![]() 。关于
。关于![]() 的方程
的方程![]() 有唯一实数解,所以方程
有唯一实数解,所以方程![]() 有且只有一个正根。方程的根分以下三种情况讨论①有且只有一个根且是正根②有一正根一负根③有一正根一零根,求m的范围。
有且只有一个正根。方程的根分以下三种情况讨论①有且只有一个根且是正根②有一正根一负根③有一正根一零根,求m的范围。
试题解析:(1)因为![]() 所以
所以![]() 所以
所以 ![]()
(2)![]() ,
,
![]()
所以![]() ,即
,即![]()
(3)因为![]() ,
, ![]()
即![]() ,所以
,所以![]() (*)
(*)
因为关于![]() 的方程
的方程![]() 有唯一实数解,所以方程(*)有且只有一个根,
有唯一实数解,所以方程(*)有且只有一个根,
令![]() ,则方程(*)变为
,则方程(*)变为![]() 有且只有一个正根,
有且只有一个正根,
①方程![]() 有且只有一个根且是正根,则
有且只有一个根且是正根,则![]()
所以![]() ,当
,当![]() 时,方程
时,方程![]() 的根为
的根为![]() 满足题意;
满足题意;
当![]() 时,方程
时,方程![]() 的根为
的根为![]() 不满足题意
不满足题意
分
②方程![]() 有一正根一负根,则
有一正根一负根,则![]() ,所以
,所以![]()
③方程![]() 有一正根一零根,则
有一正根一零根,则![]() ,所以
,所以![]() ,此时
,此时![]() 满足题意
满足题意
综上, ![]() 的范围为
的范围为![]() 或
或![]()
说明:本题第(1)问中,利用特殊值法求解也正确。


科目:高中数学 来源: 题型:
【题目】为提高信息在传输中的抗干扰能力,通常在原信息中按一定规则加入相关数据组成传输信息,设定原信息为a0a1a2 , ai∈{0,1}(i=0,1,2),传输信息为h0a0a1a2h1 , 其中h0=a0⊕a1 , h1=h0⊕a2 . ⊕运算规则为:0⊕0=0,0⊕1=1,1⊕0=1,1⊕1=0,例如原信息为111,则传输信息为01111.传输信息在传输过程中受到干扰可能导致接收信息出错,则下列接收信息一定有误的是( )
A.10111
B.01100
C.11010
D.00011
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为D的函数![]() ,若同时满足下列条件:①
,若同时满足下列条件:①![]() 在D内单调递增或单调递减;②存在区间
在D内单调递增或单调递减;②存在区间![]() ,使
,使![]() 在
在![]() 上的值域为
上的值域为![]() ,则把
,则把![]() 叫闭函数。
叫闭函数。
(1)求闭函数![]() 符合条件②的区间
符合条件②的区间![]() ;
;
(2)判断函数![]() 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)已知![]() 是正整数,且定义在
是正整数,且定义在![]() 的函数
的函数![]() 是闭函数,求正整数
是闭函数,求正整数![]() 的最小值,及此时实数k的取值范围。
的最小值,及此时实数k的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在单调递增数列![]() 中,
中,![]() ,
,![]() ,且
,且![]() 成等差数列,
成等差数列,![]() 成等比数列,
成等比数列,![]() 。
。
(Ⅰ)(ⅰ)求证:数列![]() 为等差数列;
为等差数列;
(ⅱ)求数列![]() 的通项公式。
的通项公式。
(Ⅱ)设数列![]() 的前
的前![]() 项和为
项和为![]() ,证明:
,证明:![]() ,
,![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图所示,将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知|AB|=3米,|AD|=2米。

(1)要使矩形AMPN的面积大于32平方米,则AN的长应在什么范围内?
(2)当AN的长度是多少时,矩形AMPN的面积最小?并求出最小面积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近几年骑车锻炼越来越受到人们的喜爱,男女老少踊跃参加,我校课外活动小组利用春节放假时间进行社会实践,对![]() 年龄段的人群随机抽取
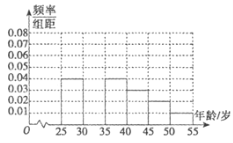
年龄段的人群随机抽取![]() 人进行了一次“你是否喜欢骑车锻炼”的问卷,将被调查人员分为“喜欢骑车”和“不喜欢骑车”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次“你是否喜欢骑车锻炼”的问卷,将被调查人员分为“喜欢骑车”和“不喜欢骑车”,得到如下统计表和各年龄段人数频率分布直方图:
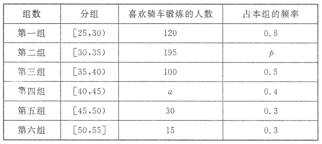
(1)补全频率分布直方图,并![]() 的值;
的值;
(2)从![]() 岁年龄段的“喜欢骑车”中采用分层抽样法抽取6人参加骑车锻炼体验活动,求其中选取2名领队来自同一组的概率。
岁年龄段的“喜欢骑车”中采用分层抽样法抽取6人参加骑车锻炼体验活动,求其中选取2名领队来自同一组的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校体育教研组研发了一项新的课外活动项目,为了解该项目受欢迎程度,在某班男生女生中各随机抽取![]() 名学生进行调研, 统计得到如下列联表:
名学生进行调研, 统计得到如下列联表:
喜欢 | 不喜欢 | 总计 | |
女生 |
| ||
男生 |
|
| |
总计 |
附:参考公式及数据
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

(1)在喜欢这项课外活动项目的学生中任选![]() 人,求选到男生的概率;
人,求选到男生的概率;
(2)根据题目要求,完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“喜欢该活动项目与性别有关”?
的把握认为“喜欢该活动项目与性别有关”?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com