
【题目】在单调递增数列![]() 中,
中,![]() ,
,![]() ,且
,且![]() 成等差数列,
成等差数列,![]() 成等比数列,
成等比数列,![]() 。
。
(Ⅰ)(ⅰ)求证:数列![]() 为等差数列;
为等差数列;
(ⅱ)求数列![]() 的通项公式。
的通项公式。
(Ⅱ)设数列![]() 的前
的前![]() 项和为
项和为![]() ,证明:
,证明:![]() ,
,![]() 。
。
【答案】(1)紧扣等差数列定义证明,(2)当![]() 为偶数时
为偶数时![]()
![]() ,当
,当![]() 为奇数时
为奇数时![]()
![]() 。(3)证明见解析。
。(3)证明见解析。
【解析】
试题分析:要证明数列![]() 为等差数列,只需证明
为等差数列,只需证明![]()
![]() 成立,由于数列首项为正,
成立,由于数列首项为正,
数列为单调递增,说以![]() ,由
,由![]() 成等差数列,得
成等差数列,得![]() ……(1),由因为
……(1),由因为![]()
![]() ,
,![]() 成等比数列,则
成等比数列,则![]() ,
,![]() 于是
于是![]() 代入(1)式整理得:
代入(1)式整理得:![]()
![]() 得证;先求
得证;先求![]() ,
,![]() 备用,由于数列
备用,由于数列![]() 为等差数列,可借助等差数列通项公式求出
为等差数列,可借助等差数列通项公式求出![]() ,再由
,再由![]() 求出
求出![]() ,最后分
,最后分![]() 为奇数和偶数两种情况表达
为奇数和偶数两种情况表达![]() ,由于数列的通项公式分
,由于数列的通项公式分![]() 为奇数和偶数两种情况表达的,所以需要合在一起,合成公式是
为奇数和偶数两种情况表达的,所以需要合在一起,合成公式是![]()
![]() ,合成后对
,合成后对![]() 进行放缩,这里技巧很重要,
进行放缩,这里技巧很重要,![]()
![]()
![]() ,再求
,再求![]() ,最后利用裂项相消法求和达到证明不等式的目的;
,最后利用裂项相消法求和达到证明不等式的目的;
试题解析:(ⅰ)因为数列![]() 为单调递增数列,
为单调递增数列,![]() ,所以
,所以![]() (
(![]() )。由题意
)。由题意![]() 成等差数列,
成等差数列,![]() 成等比数列,
成等比数列,![]() .得
.得![]()
![]() ,
,![]() ,于是
,于是![]()
![]() ,化简得
,化简得![]()
![]() ,所以数列
,所以数列![]() 为等差数列。
为等差数列。
(ⅱ)又![]() ,
,![]() ,所以数列
,所以数列![]() 的首项为
的首项为![]() ,公差为
,公差为![]() ,所以
,所以![]() ,从而
,从而![]() 。结合
。结合![]() 可得
可得![]() 。因此,当
。因此,当![]() 为偶数时
为偶数时![]()
![]() ,当
,当![]() 为奇数时
为奇数时![]()
![]() 。
。
(2)所以数列![]() 的通项公式为:
的通项公式为:
![]()
![]() 。因
。因![]()
![]()
![]() ,所以
,所以![]() ;则有
;则有![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,所以
,所以![]() ,
,![]() 。
。


 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:
【题目】已知命题p:x∈R,sinx≤1,则¬p为( )
A.x∈R,sinx≥1
B.x∈R,sinx≥1
C.x∈R,sinx>1
D.x∈R,sinx>1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A. 如果两条直线都平行于同一个平面,那么这两条直线互相平行
B. 过一条直线有且只有一个平面与已知平面垂直
C. 如果一条直线平行于一个平面内的一条直线,那么这条直线平行于这个平面
D. 如果两条直线都垂直于同一平面,那么这两条直线共面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一房产商竞标得一块扇形![]() 地皮,其圆心角
地皮,其圆心角![]()
![]() ,半径为
,半径为![]()
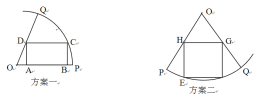
![]() ,房产商欲在此地皮上修建一栋平面图为矩形的商住楼,为使得地皮的使用率最大,准备了两种设计方案如图,方案一:矩形
,房产商欲在此地皮上修建一栋平面图为矩形的商住楼,为使得地皮的使用率最大,准备了两种设计方案如图,方案一:矩形![]() 的一边
的一边![]() 在半径
在半径![]() 上,
上,![]() 在圆弧上,
在圆弧上,![]() 在半径
在半径![]() ;方案二:矩形EFGH的顶点在圆弧上,顶点
;方案二:矩形EFGH的顶点在圆弧上,顶点![]() 分别在两条半径上。请你通过计算,为房产商提供决策建议。
分别在两条半径上。请你通过计算,为房产商提供决策建议。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知小矩形花坛ABCD中,AB=3m,AD=2m,现要将小矩形花坛建成大矩形花坛AMPN,使点B在AM上,点D在AN上,且对角线MN过点C.

(1)要使矩形AMPN的面积大于32m2,AN的长应在什么范围内?
(2)M,N是否存在这样的位置,使矩形AMPN的面积最小?若存在,求出这个最小面积及相应的AM。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知函数![]() ,
,![]() 。
。
(1)若函数![]() 在
在![]() 处的切线与函数
处的切线与函数![]() 在
在![]() 处的切线互相平行,求实数
处的切线互相平行,求实数![]() 的值;
的值;
(2)设函数![]() 。
。
(ⅰ)当实数![]() 时,试判断函数
时,试判断函数![]() 在
在![]() 上的单调性;
上的单调性;
(ⅱ)如果![]() 是
是![]() 的两个零点,
的两个零点,![]() 为函数
为函数![]() 的导函数,证明:
的导函数,证明:![]() 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com