
【题目】已知函数f(x)=sin(2x+ ![]() )+sin(2x﹣
)+sin(2x﹣ ![]() )+2cos2x﹣1,x∈R.
)+2cos2x﹣1,x∈R.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)在区间[ ![]() ]上的最大值和最小值.
]上的最大值和最小值.
【答案】
(1)解:∵f(x)=sin2xcos ![]() +cos2xsin
+cos2xsin ![]() +sin2xcos
+sin2xcos ![]() ﹣cos2xsin
﹣cos2xsin ![]() +cos2x
+cos2x
=sin2x+cos2x
= ![]() sin(2x+
sin(2x+ ![]() ),
),
∴函数f(x)的最小正周期T= ![]() =π
=π
(2)解:∵函数f(x)在区间[ ![]() ]上是增函数,在区间[
]上是增函数,在区间[ ![]() ,
, ![]() ]上是减函数,
]上是减函数,
又f(﹣ ![]() )=﹣1,f(
)=﹣1,f( ![]() )=
)= ![]() ,f(
,f( ![]() )=1,
)=1,
∴函数f(x)在区间[ ![]() ]上的最大值为
]上的最大值为 ![]() ,最小值为﹣1
,最小值为﹣1
【解析】(1)利用正弦函数的两角和与差的公式与辅助角公式将f(x)=sin(2x+ ![]() )+sin(2x﹣
)+sin(2x﹣ ![]() )+2cos2x﹣1化为f(x)=
)+2cos2x﹣1化为f(x)= ![]() sin(2x+
sin(2x+ ![]() ),即可求得函数f(x)的最小正周期;(2)可分析得到函数f(x)在区间[
),即可求得函数f(x)的最小正周期;(2)可分析得到函数f(x)在区间[ ![]() ]上是增函数,在区间[
]上是增函数,在区间[ ![]() ,
, ![]() ]上是减函数,从而可求得f(x)在区间[
]上是减函数,从而可求得f(x)在区间[ ![]() ]上的最大值和最小值.
]上的最大值和最小值.
【考点精析】利用三角函数的最值对题目进行判断即可得到答案,需要熟知函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() .
.


科目:高中数学 来源: 题型:
【题目】为保障高考的公平性,高考时每个考点都要安装手机屏蔽仪,要求在考点周围1 km内不能收到手机信号,检查员抽查某市一考点,在考点正西约![]() km/h的的B处有一条北偏东60°方向的公路,在此处检查员用手机接通电话,以每小时12千米的速度沿公路行驶,最多需要多少时间,检查员开始收不到信号,并至少持续多长时间该考点才算合格?
km/h的的B处有一条北偏东60°方向的公路,在此处检查员用手机接通电话,以每小时12千米的速度沿公路行驶,最多需要多少时间,检查员开始收不到信号,并至少持续多长时间该考点才算合格?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,单位圆
中,单位圆![]() 上存在两点
上存在两点![]() ,满足
,满足![]() 均与
均与![]() 轴垂直,设
轴垂直,设![]() 与
与![]() 的面积之和记为
的面积之和记为![]() .
.
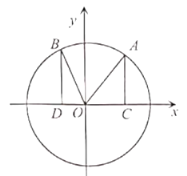
![]() 若
若![]() ,求
,求![]() 的值;
的值;
![]() 若对任意的
若对任意的![]() ,存在
,存在![]() ,使得
,使得![]() 成立,且实数
成立,且实数![]() 使得数列
使得数列![]() 为递增数列,其中
为递增数列,其中![]() 求实数
求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:

则下面结论中不正确的是
A. 新农村建设后,种植收入减少
B. 新农村建设后,其他收入增加了一倍以上
C. 新农村建设后,养殖收入增加了一倍
D. 新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关统计知识的四个命题正确的是( )
A. 衡量两变量之间线性相关关系的相关系数![]() 越接近
越接近![]() ,说明两变量间线性关系越密切
,说明两变量间线性关系越密切
B. 在回归分析中,可以用卡方![]() 来刻画回归的效果,
来刻画回归的效果,![]() 越大,模型的拟合效果越差
越大,模型的拟合效果越差
C. 线性回归方程对应的直线![]() 至少经过其样本数据点中的一个点
至少经过其样本数据点中的一个点
D. 线性回归方程![]() 中,变量
中,变量![]() 每增加一个单位时,变量
每增加一个单位时,变量![]() 平均增加
平均增加![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
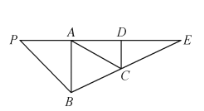
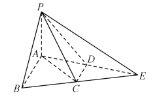
【题目】如图,在![]() 中,
中,![]() ,D是AE的中点,C是线段BE上的一点,且
,D是AE的中点,C是线段BE上的一点,且![]() ,
,![]() ,将
,将![]() 沿AB折起使得二面角
沿AB折起使得二面角![]() 是直二面角.
是直二面角.
(l)求证:CD平面PAB;
(2)求直线PE与平面PCD所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)在R上是单调递减的一次函数,且f(f(x))=4x-1.
(1)求f(x);
(2)求函数y=f(x)+x2-x在x∈[-1,2]上的最大值与最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com