
【题目】美国对中国芯片的技术封锁,这却激发了中国“芯”的研究热潮,中国华为公司研发的![]() 、
、![]() 两种芯片都已获得成功.该公司研发芯片已经耗费资金
两种芯片都已获得成功.该公司研发芯片已经耗费资金![]() 千万元,现在准备投入资金进行生产,经市场调查与预测,生产
千万元,现在准备投入资金进行生产,经市场调查与预测,生产![]() 芯片的毛收入与投入的资金成正比,已知每投入
芯片的毛收入与投入的资金成正比,已知每投入![]() 千万元,公司获得毛收入
千万元,公司获得毛收入![]() 千万元;生产
千万元;生产![]() 芯片的毛收入
芯片的毛收入![]() (千万元)与投入的资金
(千万元)与投入的资金![]() (千万元)的函数关系为
(千万元)的函数关系为![]() (
(![]() 与
与![]() 都为常数),其图象如图所示.
都为常数),其图象如图所示.
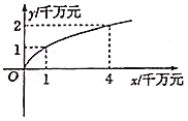
(1)试分别求出生产![]() 、
、![]() 两种芯片的毛收入
两种芯片的毛收入![]() (千万元)与投入资金
(千万元)与投入资金![]() (千万元)函数关系式;
(千万元)函数关系式;
(2)现在公司准备投入![]() 亿元资金同时生产
亿元资金同时生产![]() 、
、![]() 两种芯片,设投入
两种芯片,设投入![]() 千万元生产
千万元生产![]() 芯片,用
芯片,用![]() 表示公司所获利润,当
表示公司所获利润,当![]() 为多少时,可以获得最大利润?并求最大利润.(利润
为多少时,可以获得最大利润?并求最大利润.(利润![]() 芯片毛收入
芯片毛收入![]() 芯片毛收入
芯片毛收入![]() 研发耗费资金)
研发耗费资金)
【答案】(1)生产![]() 、
、![]() 两种芯片的毛收入
两种芯片的毛收入![]() (千万元)与投入资金
(千万元)与投入资金![]() (千万元)函数关系式分别为
(千万元)函数关系式分别为![]() 、
、![]() ;
;
(2)当![]() 时,利润最大,最大利润为
时,利润最大,最大利润为![]() 千万元.
千万元.
【解析】
(1)由题意得出生产![]() 种芯片的毛收入
种芯片的毛收入![]() (千万元)与投入资金
(千万元)与投入资金![]() (千万元)函数关系式,将点
(千万元)函数关系式,将点![]() 、
、![]() 的坐标代入函数
的坐标代入函数![]() 的解析式,求出
的解析式,求出![]() 、
、![]() 的值,可得出生产
的值,可得出生产![]() 种芯片的毛收入
种芯片的毛收入![]() (千万元)与投入资金
(千万元)与投入资金![]() (千万元)函数关系式;
(千万元)函数关系式;
(2)由题意可得出![]() ,利用二次函数的基本性质求解即可.
,利用二次函数的基本性质求解即可.
(1)由题意可知,生产![]() 种芯片的毛收入
种芯片的毛收入![]() (千万元)与投入资金
(千万元)与投入资金![]() (千万元)函数关系式为
(千万元)函数关系式为![]() ,
,
将点![]() 、
、![]() 的坐标代入函数
的坐标代入函数![]() 的解析式,得
的解析式,得![]() ,解得
,解得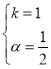 ,
,
因此,生产![]() 种芯片的毛收入
种芯片的毛收入![]() (千万元)与投入资金
(千万元)与投入资金![]() (千万元)函数关系式为
(千万元)函数关系式为![]() ;
;
(2)由题意可得![]() ,
,
![]() ,当
,当![]() 时,即当
时,即当![]() 时,函数
时,函数![]() 取得最大值,
取得最大值,
即![]() .
.
因此,当![]() 时,利润最大,且最大利润为
时,利润最大,且最大利润为![]() 千万元.
千万元.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:
【题目】如图,将宽和长都分别为x,![]() 的两个矩形部分重叠放在一起后形成的正十字形面积为
的两个矩形部分重叠放在一起后形成的正十字形面积为![]() 注:正十字形指的是原来的两个矩形的顶点都在同一个圆上,且两矩形长所在的直线互相垂直的图形
注:正十字形指的是原来的两个矩形的顶点都在同一个圆上,且两矩形长所在的直线互相垂直的图形![]() ,
,
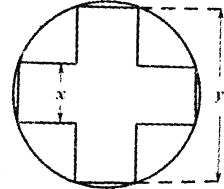
![]() 求y关于x的函数解析式;
求y关于x的函数解析式;
![]() 当x,y取何值时,该正十字形的外接圆面积最小,并求出其最小值.
当x,y取何值时,该正十字形的外接圆面积最小,并求出其最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2ax-![]() x2-3ln x,其中a∈R,为常数.
x2-3ln x,其中a∈R,为常数.
(1)若f(x)在x∈[1,+∞)上是减函数,求实数a的取值范围;
(2)若x=3是f(x)的极值点,求f(x)在x∈[1,a]上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点为原点,其焦点
的顶点为原点,其焦点![]() 到直线
到直线![]() 的距离为
的距离为![]() .设
.设![]() 为直线
为直线![]() 上的点,过点
上的点,过点![]() 作抛物线
作抛物线![]() 的两条切线
的两条切线![]() ,其中
,其中![]() 为切点.
为切点.
(1) 求抛物线![]() 的方程;
的方程;
(2) 当点![]() 为直线
为直线![]() 上的定点时,求直线
上的定点时,求直线![]() 的方程;
的方程;
(3) 当点![]() 在直线
在直线![]() 上移动时,求
上移动时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知倾斜角为
中,已知倾斜角为![]() 的直线
的直线![]() 经过点
经过点![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(1)写出曲线![]() 的普通方程;
的普通方程;
(2)若直线![]() 与曲线
与曲线![]() 有两个不同的交点
有两个不同的交点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高二年级期末考试的学生中抽出60名学生,并统计了他们的物理成绩(成绩均为整数且满分为100分),把其中不低于50分的分成五段![]() ,
,![]() ,……,
,……,![]() 后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:

(1)求出物理成绩低于50分的学生人数;
(2)估计这次考试物理学科及格率(60分以上为及格);
(3)从物理成绩不及格的学生中选x人,其中恰有一位成绩不低于50分的概率为![]() ,求此时x的值;
,求此时x的值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com