
【题目】随着通识教育理念的推广及高校课程改革的深入,选修课越来越受到人们的重视.国内一些知名院校在公共选修课的设置方面做了许多有益的探索,并且取得了一定的成果.因为选修课的课程建设处于探索阶段,选修课的教学、管理还存在很多的问题,所以需要在通识教育的基础上制定科学的、可行的解决方案,为学校选修课程的改革与创新、课程设置、考试考核、人才培养提供参考.某高校采用分层抽样法抽取了数学专业的50名参加选修课与不参加选修课的学生的成绩,统计数据如下表:
成绩优秀 | 成绩不够优秀 | 总计 | |
参加选修课 | 16 | 9 | 25 |
不参加选修课 | 8 | 17 | 25 |
总计 | 24 | 26 | 50 |
(1)试运用独立性检验的思想方法你能否有99%的把握认为“学生的成绩优秀与是否参加选修课有关”,并说明理由;
(2)如果从数学专业随机抽取5名学生,求抽到参加选修课的学生人数![]() 的分布列和数学期望(将频率当做概率计算).
的分布列和数学期望(将频率当做概率计算).
参考公式: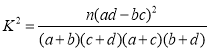 ,其中
,其中![]() .
.
临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【答案】(1)没有99%的把握认为“学生的成绩优秀与是否参加选修课有关;(2)分布列见解析,![]()
【解析】
(1)由卡方公式计算![]() ,再与临界值表对照可得结论;
,再与临界值表对照可得结论;
(2)由题意知,数学专业中参加选修课的学生的概率为![]() .随机抽取5名学生,抽到参加选修课的学生人数的所有可能取值为0,1,2,3,4,5,利用二项分布的概率公式可计算出概率得分布列,由期望公式可求得期望.
.随机抽取5名学生,抽到参加选修课的学生人数的所有可能取值为0,1,2,3,4,5,利用二项分布的概率公式可计算出概率得分布列,由期望公式可求得期望.
(1)由题意知,![]() .
.
![]() 没有99%的把握认为“学生的成绩优秀与是否参加选修课有关”
没有99%的把握认为“学生的成绩优秀与是否参加选修课有关”
(2)由题意知,数学专业中参加选修课的学生的概率为![]() .
.
随机抽取5名学生,抽到参加选修课的学生人数的所有可能取值为0,1,2,3,4,5.
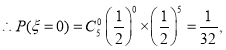
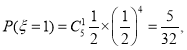
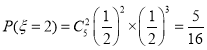
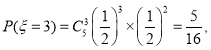
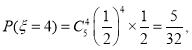
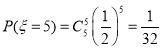
![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 | 4 | 5 |
P |
|
|
|
|
|
|
![]()


科目:高中数学 来源: 题型:
【题目】一幢高楼上安放了一块高约10 米的 LED 广告屏,一测量爱好者在与高楼底部同一水平线上的 C 处测得广告屏顶端A 处的仰角为 31.80°,再向大楼前进 20 米到 D 处,测得广告屏顶端 A 处的仰角为 37.38°(人的高度忽略不计).
(1)求大楼的高度(从地面到广告屏顶端)(精确到 1 米);
(2)若大楼的前方是一片公园空地,空地上可以安放一些长椅,为使坐在其中一个长椅上观看广告屏最清晰(长 椅的高度忽略不计),长椅需安置在距大楼底部 E 处多远?已知视角 ∠AMB( M 为观测者的位置, B 为广告屏 底部)越大,观看得越清晰.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴,直线
轴正半轴为极轴,直线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 交圆
交圆![]() 于
于![]() 两点,
两点,![]() 为
为![]() 中点.
中点.
(1)求点![]() 轨迹的极坐标方程;
轨迹的极坐标方程;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,梯形![]() 中,
中,![]() ,过
,过![]() 分别作
分别作![]() ,
,![]() ,垂足分别为
,垂足分别为![]() 、
、![]() .
.![]() ,
,![]() ,已知
,已知![]() ,将梯形
,将梯形![]() 沿
沿![]() ,
,![]() 同侧折起,得空间几何体
同侧折起,得空间几何体![]() ,如图2.
,如图2.
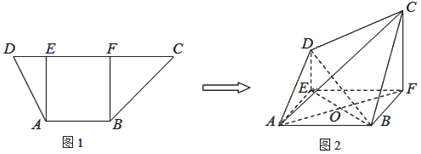
(1)若![]() ,证明:
,证明:![]() 平面
平面![]() ;
;
(2)在(1)的条件下,若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是定义在
是定义在![]() 上的函数,若对任何实数
上的函数,若对任何实数![]() 以及
以及![]() 中的任意两数
中的任意两数![]() 、
、![]() ,恒有
,恒有![]() ,则称
,则称![]() 为定义在
为定义在![]() 上的
上的![]() 函数.
函数.
(1)证明函数![]() 是定义域上的
是定义域上的![]() 函数;
函数;
(2)判断函数![]() 是否为定义域上的
是否为定义域上的![]() 函数,请说明理由;
函数,请说明理由;
(3)若![]() 是定义域为
是定义域为![]() 的函数,且最小正周期为
的函数,且最小正周期为![]() ,试证明
,试证明![]() 不是
不是![]() 上的
上的![]() 函数.
函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业在“精准扶贫”行动中,决定帮助一贫困山区将水果运出销售.现有8辆甲型车和4辆乙型车,甲型车每次最多能运6吨且每天能运4次,乙型车每次最多能运10吨且每天能运3次,甲型车每天费用320元,乙型车每天费用504元.若需要一天内把180吨水果运输到火车站,则通过合理调配车辆运送这批水果的费用最少为______元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]() ,记
,记![]()
![]() ;
;
(1)求实数![]() 、
、![]() 的值;
的值;
(2)若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的范围;
的范围;
(3)对于定义在![]() 上的函数
上的函数![]() ,设
,设![]() ,
,![]() ,用任意的
,用任意的![]()
![]() 将
将![]() 划分为
划分为![]() 个小区间,其中
个小区间,其中![]() ,若存在一个常数
,若存在一个常数![]() ,使得
,使得![]()
![]() 恒成立,则称函数
恒成立,则称函数![]() 为
为![]() 上的有界变差函数;
上的有界变差函数;
①试证明函数![]() 是在
是在![]() 上的有界变差函数,并求出
上的有界变差函数,并求出![]() 的最小值;
的最小值;
②写出![]() 是在
是在![]() 上的有界变差函数的一个充分条件,使上述结论成为其特例;(不要求证明)
上的有界变差函数的一个充分条件,使上述结论成为其特例;(不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明与另外2名同学进行“手心手背”游戏,规则是:3人同时随机等可能选择手心或手背中的一种手势,规定相同手势人数多者每人得1分,其余每人得0分.现3人共进行了4次游戏,记小明4次游戏得分之和为![]() ,则
,则![]() 的期望为( )
的期望为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义max{x1,x2,x3,…,xn}表示x1,x2,x3,…,xn中的最大值.已知数列an=![]() ,bn=
,bn=![]() ,cn=
,cn=![]() ,其中n+m+p=200,m=kn,n,m,p,k∈N*.记dn=max{an,bn,cn}
,其中n+m+p=200,m=kn,n,m,p,k∈N*.记dn=max{an,bn,cn}
(Ⅰ)求max{an,bn}
(Ⅱ)当k=2时,求dn的最小值;
(Ⅲ)k∈N*,求dn的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com