
【题目】设过抛物线![]() 的焦点
的焦点![]() 的直线
的直线![]() 交抛物线于点
交抛物线于点![]() ,若以
,若以![]() 为直径的圆过点
为直径的圆过点![]() ,且与
,且与![]() 轴交于
轴交于![]() ,
, ![]() 两点,则
两点,则![]() ( )
( )
A. 3 B. 2 C. -3 D. -2
【答案】C
【解析】抛物线焦点坐标为F(1,0),准线方程为x=﹣1
设直线MN的方程为x=ty+1,A、B的坐标分别为(![]() ,y1),(
,y1),(![]() ,y2)
,y2)
联立直线和抛物线得到方程:y2﹣4my﹣4=0,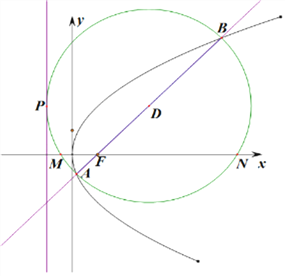
∴y1+y2=4m,y1y2=﹣4,
x1+x2=ty1+1+ty2+1=t(y1+y2)+2=4t2+2, ![]() =2t2+1,
=2t2+1, ![]() =2t,
=2t,
则圆心D(2t2+1,2t),
由抛物线的性质可知:丨AB丨=x1+x2+p=4(t2+1),
由P到圆心的距离d=![]() ,由题意可知:d=
,由题意可知:d=![]() 丨AB丨,
丨AB丨,
解得:t=1,则圆心为(3,2),半径为4,∴圆的方程方程为(x﹣3)2+(y﹣2)2=42,
则当y=0,求得与x轴的交点坐标,假设m>n,则m=3﹣2![]() ,n=3+2
,n=3+2![]() ,
,
∴mn=(3﹣2![]() )(3+2
)(3+2![]() )=﹣3,
)=﹣3,
故选:C.


科目:高中数学 来源: 题型:
【题目】三棱锥P﹣ABC中,底面△ABC满足BA=BC, ![]() ,P在面ABC的射影为AC的中点,且该三棱锥的体积为
,P在面ABC的射影为AC的中点,且该三棱锥的体积为 ![]() ,当其外接球的表面积最小时,P到面ABC的距离为( )
,当其外接球的表面积最小时,P到面ABC的距离为( )
A.2
B.3
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年3月14日,“![]() 共享单车”终于来到芜湖,
共享单车”终于来到芜湖,![]() 共享单车又被亲切称作“小黄车”是全球第一个无桩共享单车平台,开创了首个“单车共享”模式.相关部门准备对该项目进行考核,考核的硬性指标是:市民对该项目的满意指数不低于
共享单车又被亲切称作“小黄车”是全球第一个无桩共享单车平台,开创了首个“单车共享”模式.相关部门准备对该项目进行考核,考核的硬性指标是:市民对该项目的满意指数不低于![]() ,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,随机访问了使用共享单车的
,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,随机访问了使用共享单车的![]() 名市民,并根据这
名市民,并根据这![]() 名市民对该项目满意程度的评分(满分
名市民对该项目满意程度的评分(满分![]() 分),绘制了如下频率分布直方图:
分),绘制了如下频率分布直方图:

(I)为了了解部分市民对“共享单车”评分较低的原因,该部门从评分低于![]() 分的市民中随机抽取
分的市民中随机抽取![]() 人进行座谈,求这
人进行座谈,求这![]() 人评分恰好都在
人评分恰好都在![]() 的概率;
的概率;
(II)根据你所学的统计知识,判断该项目能否通过考核,并说明理由.
(注:满意指数=![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】棉花的纤维长度是评价棉花质量的重要指标,某农科所的专家在土壤环境不同的甲、乙两块实验地分别种植某品种的棉花,为了评价该品种的棉花质量,在棉花成熟后,分别从甲、乙两地的棉花中各随机抽取20根棉花纤维进行统计,结果如下表:(记纤维长度不低于300mm的为“长纤维”,其余为“短纤维”)
纤维长度 | (0,100) | [100,200) | [200,300) | [300,400) | [400,500] |
甲地(根数) | 3 | 4 | 4 | 5 | 4 |
乙地(根数) | 1 | 1 | 2 | 10 | 6 |
(1)由以上统计数据,填写下面2×2列联表,并判断能否在犯错误概率不超过0.025的前提下认为“纤维长度与土壤环境有关系”.
甲地 | 乙地 | 总计 | |
长纤维 | |||
短纤维 | |||
总计 |
附:(1) ![]() ;(2)临界值表;
;(2)临界值表;
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(2)现从上述40根纤维中,按纤维长度是否为“长纤维”还是“短纤维”采用分层抽样的方法抽取8根进行检测,在这8根纤维中,记乙地“短纤维”的根数为X,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市医疗保险实行定点医疗制度,按照“就近就医、方便管理” 的原则,规定参加保险人员可自主选择四家医疗保险定点医院和一家社区医院作为就诊的医疗机构.若甲、乙、丙、丁4名参加保险人员所在地区附近有![]() 三家社区医院,并且他们的选择是等可能的、相互独立的.
三家社区医院,并且他们的选择是等可能的、相互独立的.
(1)求甲、乙两人都选择![]() 社区医院的概率;
社区医院的概率;
(2)求甲、乙两人不选择同一家社区医院的概率;
(3)设在4名参加保险人员中选择![]() 社区医院的人数为
社区医院的人数为![]() ,求
,求![]() 的分布列和数学期望及方差.
的分布列和数学期望及方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+(y-1)2=5,直线l:mx-y+1-m=0(m∈R).
(1)判断直线l与圆C的位置关系;
(2)设直线l与圆C交于A,B两点,若直线l的倾斜角为120°,求弦AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面ABCD是平行四边形,侧面PAD是边长为2的正三角形,AB=BD= ![]() ,PB=
,PB= ![]()
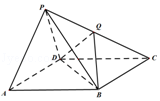
(Ⅰ)求证:平面PAD⊥平面ABCD;
(Ⅱ)设Q是棱PC上的点,当PA∥平面BDQ时,求二面角A﹣BD﹣Q的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在直角梯形![]() 中,
中,![]() ,
,![]() ,且
,且![]() .现以
.现以![]() 为一边向形外作正方形
为一边向形外作正方形![]() ,然后沿边
,然后沿边![]() 将正方形
将正方形![]() 翻折,使平面
翻折,使平面![]() 与平面
与平面![]() 垂直,
垂直,![]() 为
为![]() 的中点,如图2.
的中点,如图2.

(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com