
【题目】如图,已知圆![]() 的半径为
的半径为![]() ,
,![]() ,
,![]() 是圆
是圆![]() 上的一个动点,
上的一个动点,![]() 的中垂线
的中垂线![]() 交
交![]() 于点
于点![]() ,以直线
,以直线![]() 为
为![]() 轴,
轴,![]() 的中垂线为
的中垂线为![]() 轴建立平面直角坐标系。
轴建立平面直角坐标系。

(Ⅰ)若点![]() 的轨迹为曲线
的轨迹为曲线![]() ,求曲线
,求曲线![]() 的方程;
的方程;
(Ⅱ)设点![]() 为圆
为圆![]() 上任意一点,过
上任意一点,过![]() 作圆
作圆![]() 的切线与曲线
的切线与曲线![]() 交于
交于![]() 两点,证明:以
两点,证明:以![]() 为直径的圆经过定点,并求出该定点的坐标。
为直径的圆经过定点,并求出该定点的坐标。
【答案】(Ⅰ)![]() ;(Ⅱ)见解析.
;(Ⅱ)见解析.
【解析】
(Ⅰ)根据中垂线性质得出:![]() ,从而知
,从而知![]() 点轨迹是椭圆,由椭圆标准方程可得.
点轨迹是椭圆,由椭圆标准方程可得.
(Ⅱ)当切线斜率不存在时,可得两圆,它们的交点为原点![]() ,接着证明其它的圆都过原点即可,即证
,接着证明其它的圆都过原点即可,即证![]() ,也即证
,也即证![]() ,为此可设直线
,为此可设直线![]() 方程为
方程为![]() ,由直线与圆相切得
,由直线与圆相切得![]() 关系式,设
关系式,设![]() ,由直线方程与椭圆方程联立化简可得
,由直线方程与椭圆方程联立化简可得![]() ,计算
,计算![]() 可得结论.
可得结论.
(Ⅰ)因为![]() 是线段
是线段![]() 中垂线上的点,所以
中垂线上的点,所以![]()
所以:![]()
所以:点![]() 的轨迹是以
的轨迹是以![]() 为焦点的椭圆
为焦点的椭圆
于是:![]() ,于是
,于是![]()
所以:曲线![]() 的方程是
的方程是![]()
(Ⅱ)当直线![]() 斜率不存在时,
斜率不存在时,
取![]() ,则
,则![]() ,此时圆的方程是
,此时圆的方程是![]()
取![]() ,则
,则![]() ,此时圆的方程是
,此时圆的方程是![]()
两圆相交于原点![]() ,下面证明原点
,下面证明原点![]() 满足题目条件,即证:
满足题目条件,即证:![]()
当直线![]() 斜率不存在时,设直线方程为
斜率不存在时,设直线方程为![]()
因为直线与圆相切,所以圆心到直线的距离![]() ,即
,即![]() ①
①
由![]() 可得:
可得:![]()
设![]() ,则
,则![]()
于是:![]()
所以:![]()
将①代入可得:![]()
综上所述:以![]() 为直径的圆经过定点
为直径的圆经过定点![]()


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+ ![]() +lnx,a∈R. (Ⅰ)若f(x)在x=1处取得极值,求a的值;
+lnx,a∈R. (Ⅰ)若f(x)在x=1处取得极值,求a的值;
(Ⅱ)若f(x)在区间(1,2)上单调递增,求a的取值范围;
(Ⅲ)讨论函数g(x)=f'(x)﹣x的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC.O为AB的中点,OF⊥EC. (Ⅰ)求证:OE⊥FC:
(Ⅱ)若 ![]() =
= ![]() 时,求二面角F﹣CE﹣B的余弦值.
时,求二面角F﹣CE﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ,函数
,函数![]() 的最小值为
的最小值为![]() .
.
(1)求![]() ;
;
(2)是否存在实数![]() 同时满足下列条件:
同时满足下列条件:
①![]() ;
;
②当![]() 的定义域为
的定义域为![]() 时, 值域为
时, 值域为![]() ?若存在, 求出
?若存在, 求出![]() 的值;若不存在, 说明理由.
的值;若不存在, 说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义域为
是定义域为![]() 的奇函数,当
的奇函数,当![]() .
.
(Ⅰ)求出函数![]() 在
在![]() 上的解析式;
上的解析式;
(Ⅱ)在答题卷上画出函数![]() 的图象,并根据图象写出
的图象,并根据图象写出![]() 的单调区间;
的单调区间;

(Ⅲ)若关于![]() 的方程
的方程![]() 有三个不同的解,求
有三个不同的解,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学利用周末组织教职员工进行了一次秋季登山健身的活动,有N人参加,现将所有参加者按年龄情况分为[20,25),[25,30),[30,35),[35,40),[40,45),[45,50),[50,55)等七组,其频率分布直方图如下所示.已知[35,40)这组的参加者是8人. 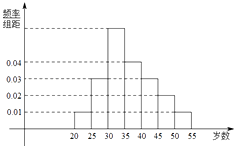
(1)求N和[30,35)这组的参加者人数N1;
(2)已知[30,35)和[35,40)这两组各有2名数学教师,现从这两个组中各选取2人担任接待工作,设两组的选择互不影响,求两组选出的人中都至少有1名数学老师的概率;
(3)组织者从[45,55)这组的参加者(其中共有4名女教师,其余全为男教师)中随机选取3名担任后勤保障工作,其中女教师的人数为x,求x的分布列和均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 分别是椭圆
分别是椭圆![]() 的左右顶点,
的左右顶点, ![]() 为其右焦点,
为其右焦点, ![]() 与
与![]() 的等比中项是
的等比中项是![]() ,椭圆的离心率为
,椭圆的离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设不过原点![]() 的直线
的直线![]() 与该轨迹交于
与该轨迹交于![]() 两点,若直线
两点,若直线![]() 的斜率依次成等比数列,求
的斜率依次成等比数列,求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC三边长构成公差为d(d≠0)的等差数列,则△ABC最大内角α的取值范围为( )
A.![]() <α≤
<α≤ ![]()
B.![]() <α<π
<α<π
C.![]() ≤α<π
≤α<π
D.![]() <α≤
<α≤ ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com