
【题目】如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC.O为AB的中点,OF⊥EC. (Ⅰ)求证:OE⊥FC:
(Ⅱ)若 ![]() =
= ![]() 时,求二面角F﹣CE﹣B的余弦值.
时,求二面角F﹣CE﹣B的余弦值.
【答案】证明:(Ⅰ)连结OC,∵AC=BC,O是AB的中点, 故OC⊥AB.
又∵平面ABC⊥平面ABEF,
故OC⊥平面ABE,于是OC⊥OF.
又OF⊥EC,∵OF⊥平面OEC,
∴OF⊥OE,
又∵OC⊥OE,∴OE⊥平面OFC,
∴OE⊥FC;
(Ⅱ)解:由(I)得AB=2AF.不妨设AF=1,AB=2,
∵ ![]() =
= ![]() ,∴AC=
,∴AC= ![]() ,则OC=
,则OC= ![]()
建立以O为坐标原点,OC,OB,OD分别为x,y,z轴的空间直角坐标系如图:
则F(0,﹣1,1),E(0,1,1),B(0,1,0),C( ![]() ,0,0),则
,0,0),则![]() =(﹣
=(﹣ ![]() ,1,1),
,1,1), ![]() =(0,﹣2,0),
=(0,﹣2,0),
设平面FCE的法向量为 ![]() =(x,y,z),
=(x,y,z),
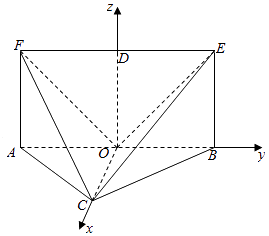
则 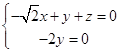 .
.
∴ ![]() =(1,0,
=(1,0, ![]() ),
),
∵ ![]() =(0,0,1),
=(0,0,1), ![]() =(
=( ![]() ,﹣1,0),
,﹣1,0),
∴同理可得平面CEB的法向量为 ![]() =(1,
=(1, ![]()
![]() ,0),
,0),
∴cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() ,
,
∵二面角F﹣CE﹣B是钝二面角,
∴二面角F﹣CE﹣B的余弦值为﹣ ![]() .
.
【解析】(Ⅰ)连结OC,则OC⊥AB,从而得到OC⊥OF,进而得到OF⊥OE,由此能证明OE⊥FC. (Ⅱ)由(I)得AB=2AF.不妨设AF=1,AB=2建立空间坐标系,求出平面的法向量,利用向量法即可.


科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,等比数列
,等比数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 的通项公式;
的通项公式;
(2)若![]() ,求
,求![]() .
.
【答案】(1)![]() ;(2)21或
;(2)21或![]() .
.
【解析】试题分析:(1)设等差数列![]() 公差为
公差为![]() ,等比数列
,等比数列![]() 公比为
公比为![]() ,由已知条件求出
,由已知条件求出![]() ,再写出通项公式;(2)由
,再写出通项公式;(2)由![]() ,求出
,求出![]() 的值,再求出
的值,再求出![]() 的值,求出
的值,求出![]() 。
。
试题解析:设等差数列![]() 公差为
公差为![]() ,等比数列
,等比数列![]() 公比为
公比为![]() 有
有![]() ,即
,即![]() .
.
(1)∵![]() ,结合
,结合![]() 得
得![]() ,
,
∴![]() .
.
(2)∵![]() ,解得
,解得![]() 或3,
或3,
当![]() 时,
时,![]() ,此时
,此时![]() ;
;
当![]() 时,
时,![]() ,此时
,此时![]() .
.
【题型】解答题
【结束】
20
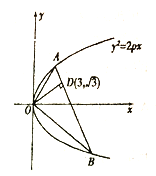
【题目】如图,已知直线与抛物线![]() 相交于
相交于![]() 两点,且
两点,且![]() ,
, ![]() 交
交![]() 于
于![]() ,且点
,且点![]() 的坐标为
的坐标为![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() 为抛物线的焦点,
为抛物线的焦点, ![]() 为抛物线上任一点,求
为抛物线上任一点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若关于x的不等式xex﹣2ax+a<0的非空解集中无整数解,则实数a的取值范围是( )
A.[ ![]() ,
, ![]() )
)
B.[ ![]() ,
, ![]() )
)
C.[ ![]() ,e]
,e]
D.[ ![]() ,e]
,e]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=ln(x+a)﹣x,曲线y=f(x)与x轴相切. (Ⅰ)求f(x)的单调区间;
(Ⅱ)是否存在实数m使得 ![]() 恒成立?若存在,求实数m的值;若不存在,说明理由.
恒成立?若存在,求实数m的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣2ax+1+b(a>0)在区间[2,3]上有最大值4和最小值1.
(Ⅰ)求实数a,b的值;
(Ⅱ)设函数g(x)=![]() ,若不等式g(2x)﹣k2x≤0在x∈[﹣1,1]上恒成立,求实数k的取值范围.
,若不等式g(2x)﹣k2x≤0在x∈[﹣1,1]上恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】最新公布的《道路交通安全法》和《道路交通安全法实施条例》对车速、安全车距以及影响驾驶人反应快慢等因素均有详细规定,这些规定说到底主要与刹车距离有关,刹车距离是指从驾驶员发现障碍到制动车辆,最后完全停止所行驶的距离,即:刹车距离=反应距离+制动距离,反应距离=反应时间×速率,制动距离与速率的平方成正比,某反应时间为![]() 的驾驶员以
的驾驶员以![]() 的速率行驶,遇紧急情况,汽车的刹车距离为
的速率行驶,遇紧急情况,汽车的刹车距离为![]() .
.
(![]() )试将刹车距离
)试将刹车距离![]() 表示为速率
表示为速率![]() 的函数.
的函数.
(![]() )若该驾驶员驾驶汽车在限速为
)若该驾驶员驾驶汽车在限速为![]() 的公路上行驶,遇紧急情况,汽车的刹车距离为
的公路上行驶,遇紧急情况,汽车的刹车距离为![]() ,试问该车是否超速?请说明理由.
,试问该车是否超速?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司共有60位员工,为提高员工的业务技术水平,公司拟聘请专业培训机构进行培训.培训的总费用由两部分组成:一部分是给每位参加员工支付400元的培训材料费;另一部分是给培训机构缴纳的培训费.若参加培训的员工人数不超过30人,则每人收取培训费1000元;若参加培训的员工人数超过30人,则每超过1人,人均培训费减少20元.设公司参加培训的员工人数为x人,此次培训的总费用为y元.
(1)求出y与x之间的函数关系式;
(2)请你预算:公司此次培训的总费用最多需要多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆![]() 的半径为
的半径为![]() ,
,![]() ,
,![]() 是圆
是圆![]() 上的一个动点,
上的一个动点,![]() 的中垂线
的中垂线![]() 交
交![]() 于点
于点![]() ,以直线
,以直线![]() 为
为![]() 轴,
轴,![]() 的中垂线为
的中垂线为![]() 轴建立平面直角坐标系。
轴建立平面直角坐标系。

(Ⅰ)若点![]() 的轨迹为曲线
的轨迹为曲线![]() ,求曲线
,求曲线![]() 的方程;
的方程;
(Ⅱ)设点![]() 为圆
为圆![]() 上任意一点,过
上任意一点,过![]() 作圆
作圆![]() 的切线与曲线
的切线与曲线![]() 交于
交于![]() 两点,证明:以
两点,证明:以![]() 为直径的圆经过定点,并求出该定点的坐标。
为直径的圆经过定点,并求出该定点的坐标。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知指数函数y=g(x)满足:g(3)=8,定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
(1)确定y=g(x),y=f(x)的解析式;
(2)若h(x)=f(x)+a在(﹣1,1)上有零点,求a的取值范围;
(3)若对任意的t∈(﹣4,4),不等式f(6t﹣3)+f(t2﹣k)<0恒成立,求实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com