
【题目】已知向量![]() ,
,![]() ,函数
,函数![]() 的最大值为
的最大值为![]() .
.
(1)求![]() 的大小;
的大小;
(2)将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的![]() ,纵坐标不变,得到函数
,纵坐标不变,得到函数![]() 的图象,作出函数
的图象,作出函数![]() 在
在![]() 的图象.
的图象.
【答案】(1)![]() ;(2)图象见解析.
;(2)图象见解析.
【解析】试题分析:(1)利用向量的数量积展开,通过二倍角公式以及两角和的正弦公式将函数化为一个角的一个三角函数的形式,通过最大值求![]() 的大小 ;(2)通过将函数
的大小 ;(2)通过将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,再将所得图象各点的横坐标缩短为原来的
个单位,再将所得图象各点的横坐标缩短为原来的![]() 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数![]() 的解析式,然后列表、描点、连线即可得到
的解析式,然后列表、描点、连线即可得到![]() 在
在![]() 的图象.
的图象.
试题解析:(1) ![]() =
=![]() Asin xcos x+
Asin xcos x+![]() cos 2x=A(
cos 2x=A(![]() sin 2x+
sin 2x+![]() cos 2x)
cos 2x)
=Asin(2x+![]() ).因为f(x)的最大值为6,A>0,所以A=6.
).因为f(x)的最大值为6,A>0,所以A=6.
(2)由(1)得f(x)=6sin(2x+![]() ).将函数y=f(x)的图象向左平移
).将函数y=f(x)的图象向左平移![]() 个单位后得到y=6sin[2(x+
个单位后得到y=6sin[2(x+![]() )+
)+![]() ]=6sin(2x+
]=6sin(2x+![]() )的图象;
)的图象;
再将得到的图象上各点的横坐标缩短为原来的![]() ,纵坐标不变,得到y=6sin(4x+
,纵坐标不变,得到y=6sin(4x+![]() )的图象.因此
)的图象.因此![]()
![]() 的图像如图所示.
的图像如图所示.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|



 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在[﹣1,1]上的奇函数,且f(1)=1,若a,b∈[﹣1,1],a+b≠0时,有 ![]() 成立.
成立.
(1)判断f(x)在[﹣1,1]上的单调性,并证明它;
(2)解不等式f(x2)<f(2x);
(3)若f(x)≤m2﹣2am+1对所有的a∈[﹣1,1]恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】综合题。
(1)利用“五点法”画出函数 ![]() 在
在 ![]() 内的简图
内的简图
x | |||||
| |||||
y |

(2)若对任意x∈[0,2π],都有f(x)﹣3<m<f(x)+3恒成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() .过原点
.过原点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点,点
两点,点![]() 是椭圆
是椭圆![]() 上的点,若
上的点,若![]() ,
, ![]() ,且
,且![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2) 设椭圆在点![]() 处的切线记为直线
处的切线记为直线![]() ,点
,点![]() 在
在![]() 上的射影分别为
上的射影分别为![]() ,过
,过![]() 作
作![]() 的垂线交
的垂线交![]() 轴于点
轴于点![]() ,试问
,试问![]() 是否为定值?若是,求出该定值;若不是,请说明理由.
是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:sin230°+sin290°+sin2150°= ![]() ;
;
sin25°+sin265°+sin2125°= ![]() ;
;
sin212°+sin272°+sin2132°= ![]() ;
;
通过观察上述两等式的规律,请你写出一般性的命题,并给予的证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产一种仪器的元件,由于受生产能力和技术水平等因素的限制,会产生一些次品,根据经验知道,次品数P(万件)与日产量x(万件)之间满足关系: 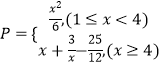 已知每生产l万件合格的元件可以盈利2万元,但每生产l万件次品将亏损1万元.(利润=盈利一亏损)
已知每生产l万件合格的元件可以盈利2万元,但每生产l万件次品将亏损1万元.(利润=盈利一亏损)
(1)试将该工厂每天生产这种元件所获得的利润T(万元)表示为日产量x(万件)的函数;
(2)当工厂将这种仪器的元件的日产量x定为多少时获得的利润最大,最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣ax2﹣bx﹣1,其中a,b∈R,e=2.71828…为自然对数的底数.
(1)设g(x)是函数f(x)的导函数,求函数g(x)在区间[0,1]上的最小值;
(2)若f(1)=0,函数f(x)在区间(0,1)内有零点,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式组 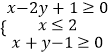 表示的平面区域为D,则
表示的平面区域为D,则
(1)z=x2+y2的最小值为 .
(2)若函数y=|2x﹣1|+m的图象上存在区域D上的点,则实数m的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域是D,若存在常数m、M,使得m≤f(x)≤M对任意x∈D成立,则称函数f(x)是D上的有界函数,其中m称为函数f(x)的下界,M称为函数f(x)的上界;特别地,若“=”成立,则m称为函数f(x)的下确界,M称为函数f(x)的上确界. (Ⅰ)判断 ![]() 是否是有界函数?说明理由;
是否是有界函数?说明理由;
(Ⅱ)若函数f(x)=1+a2x+4x(x∈(﹣∞,0))是以﹣3为下界、3为上界的有界函数,求实数a的取值范围;
(Ⅲ)若函数 ![]() ,T(a)是f(x)的上确界,求T(a)的取值范围.
,T(a)是f(x)的上确界,求T(a)的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com