
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐfΘ®xΘ©ΒΡΕ®“ε”ρ «DΘ§»τ¥φ‘Ύ≥Θ ΐmΓΔMΘ§ ΙΒΟmΓήfΘ®xΘ©ΓήMΕ‘»Έ“βxΓ D≥…ΝΔΘ§‘ρ≥ΤΚ· ΐfΘ®xΘ© «D…œΒΡ”–ΫγΚ· ΐΘ§Τδ÷–m≥ΤΈΣΚ· ΐfΘ®xΘ©ΒΡœ¬ΫγΘ§M≥ΤΈΣΚ· ΐfΘ®xΘ©ΒΡ…œΫγΘΜΧΊ±πΒΊΘ§»τΓΑ=Γ±≥…ΝΔΘ§‘ρm≥ΤΈΣΚ· ΐfΘ®xΘ©ΒΡœ¬»ΖΫγΘ§M≥ΤΈΣΚ· ΐfΘ®xΘ©ΒΡ…œ»ΖΫγΘ° Θ®ΔώΘ©≈–Εœ ![]() «Ζώ «”–ΫγΚ· ΐΘΩΥΒΟςάμ”…ΘΜ
«Ζώ «”–ΫγΚ· ΐΘΩΥΒΟςάμ”…ΘΜ
Θ®ΔρΘ©»τΚ· ΐfΘ®xΘ©=1+a2x+4xΘ®xΓ Θ®©¹ΓόΘ§0Θ©Θ© «“‘©¹3ΈΣœ¬ΫγΓΔ3ΈΣ…œΫγΒΡ”–ΫγΚ· ΐΘ§«σ Β ΐaΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®ΔσΘ©»τΚ· ΐ ![]() Θ§TΘ®aΘ© «fΘ®xΘ©ΒΡ…œ»ΖΫγΘ§«σTΘ®aΘ©ΒΡ»Γ÷ΒΖΕΈßΘ°
Θ§TΘ®aΘ© «fΘ®xΘ©ΒΡ…œ»ΖΫγΘ§«σTΘ®aΘ©ΒΡ»Γ÷ΒΖΕΈßΘ°
ΓΨ¥πΑΗΓΩΫβΘΚΘ®ΔώΘ©fΘ®xΘ©= ![]() ©¹
©¹ ![]() =
= ![]() Θ§ ΓΏxΓί0Θ§Γύ
Θ§ ΓΏxΓί0Θ§Γύ ![]() +
+ ![]() Γί1Θ§
Γί1Θ§
Γύ0ΘΦfΘ®xΘ©Γή1Θ§Κ· ΐfΘ®xΘ© «”–ΫγΚ· ΐΘ§
Ννt=3x Θ§ ‘ρtΘΨ0Θ§
Γύy=t2©¹3tΓί©¹1Φ¥gΘ®xΘ©Γ [©¹1Θ§+ΓόΘ©Θ§
ΓύgΘ®xΘ©≤Μ «”–ΫγΚ· ΐΘΜ
Θ®ΔρΘ©ΓΏΚ· ΐfΘ®xΘ©=1+a2x+4x Θ§ Θ®xΓ Θ®©¹ΓόΘ§0Θ©Θ© «“‘©¹3ΈΣœ¬ΫγΘ§3ΈΣ…œΫγΒΡ”–ΫγΚ· ΐΘ§
Γύ©¹3Γή1+a2x+4xΓή3‘ΎΘ®©¹ΓόΘ§0Θ©…œΚψ≥…ΝΔΘ§
Φ¥©¹2x©¹ ![]() ΓήaΓή
ΓήaΓή ![]() ©¹2x‘ΎΘ®©¹ΓόΘ§0Θ©…œΚψ≥…ΝΔΘ§
©¹2x‘ΎΘ®©¹ΓόΘ§0Θ©…œΚψ≥…ΝΔΘ§
Ννt=2x Θ§ gΘ®tΘ©=©¹t©¹ ![]() Θ§hΘ®tΘ©=©¹t+
Θ§hΘ®tΘ©=©¹t+ ![]() Θ§
Θ§
ΓΏxΘΦ0Θ§Γύ0ΘΦtΘΦ1Θ§
…ηt1 Θ§ t2Γ Θ®0Θ§1Θ©Θ§«“t1ΘΦt2 Θ§
‘ρgΘ®t1Θ©©¹gΘ®t2Θ©= ![]() ΘΦ0Θ§
ΘΦ0Θ§
ΓύgΘ®tΘ©‘ΎΘ®0Θ§1Θ©Βί‘ωΘ§
Ι gΘ®tΘ©ΘΦgΘ®1Θ©=©¹5Θ§ΓύaΓί©¹5Θ§hΘ®t1Θ©©¹hΘ®t2Θ©ΘΨ0Θ§
ΓύhΘ®tΘ©‘ΎΘ®0Θ§1Θ©…œ «ΦθΚ· ΐΘ§
Ι hΘ®tΘ©ΘΨhΘ®1Θ©=1Θ§
ΓύaΓή1Θ§
Ήέ…œΘ§ Β ΐaΒΡΖΕΈß «[©¹5Θ§1]ΘΜ
Θ®ΔσΘ©”…y= ![]() Θ§ΒΟΘΚa2x=
Θ§ΒΟΘΚa2x= ![]() Θ§
Θ§
ΓΏxΓ [0Θ§1]Θ§aΘΨ0Θ§
ΓύaΓήa2xΓή2aΘ§
Φ¥aΓή ![]() Γή2aΘ§
Γή2aΘ§
Γύ ![]() ΓήyΓή
ΓήyΓή ![]() Θ§
Θ§
Ι TΘ®aΘ©= ![]() =©¹1+
=©¹1+ ![]() Θ§
Θ§
ΓΏaΘΨ0Θ§
ΓύTΘ®aΘ©ΒΡΖΕΈß «Θ®©¹1Θ§1Θ©
ΓΨΫβΈωΓΩΘ®ΔώΘ©ΗυΨί”–ΫγΚ· ΐΒΡΕ®“εΖ÷±π«σ≥ωfΘ®xΘ©Θ§gΘ®xΘ©ΒΡΖΕΈßΘ§¥”Εχ≈–Εœ «Ζώ”–ΫγΦ¥Ω…ΘΜΘ®ΔρΘ©Έ ΧβΉΣΜ·ΈΣ©¹2x©¹ ![]() ΓήaΓή
ΓήaΓή ![]() ©¹2x‘ΎΘ®©¹ΓόΘ§0Θ©…œΚψ≥…ΝΔΘ§Ννt=2x Θ§ gΘ®tΘ©=©¹t©¹
©¹2x‘ΎΘ®©¹ΓόΘ§0Θ©…œΚψ≥…ΝΔΘ§Ννt=2x Θ§ gΘ®tΘ©=©¹t©¹ ![]() Θ§hΘ®tΘ©=©¹t+
Θ§hΘ®tΘ©=©¹t+ ![]() Θ§ΗυΨίΚ· ΐΒΡΒΞΒς–‘«σ≥ωtΒΡΖΕΈßΦ¥Ω…ΘΜΘ®ΔσΘ©«σ≥ωaΓή
Θ§ΗυΨίΚ· ΐΒΡΒΞΒς–‘«σ≥ωtΒΡΖΕΈßΦ¥Ω…ΘΜΘ®ΔσΘ©«σ≥ωaΓή ![]() Γή2aΘ§ΗυΨί
Γή2aΘ§ΗυΨί ![]() ΓήyΓή
ΓήyΓή ![]() Θ§ΒΟΒΫTΘ®aΘ©=
Θ§ΒΟΒΫTΘ®aΘ©= ![]() Θ§¥”Εχ«σ≥ωTΘ®aΘ©ΒΡΖΕΈßΦ¥Ω…Θ°
Θ§¥”Εχ«σ≥ωTΘ®aΘ©ΒΡΖΕΈßΦ¥Ω…Θ°
ΓΨΩΦΒψΨΪΈωΓΩάϊ”ΟΚ· ΐΒΡΉν÷ΒΦΑΤδΦΗΚΈ“β“εΕ‘ΧβΡΩΫχ––≈–ΕœΦ¥Ω…ΒΟΒΫ¥πΑΗΘ§–η“Σ λ÷Σάϊ”ΟΕΰ¥ΈΚ· ΐΒΡ–‘÷ Θ®≈δΖΫΖ®Θ©«σΚ· ΐΒΡΉν¥σΘ®–ΓΘ©÷ΒΘΜάϊ”ΟΆΦœσ«σΚ· ΐΒΡΉν¥σΘ®–ΓΘ©÷ΒΘΜάϊ”ΟΚ· ΐΒΞΒς–‘ΒΡ≈–ΕœΚ· ΐΒΡΉν¥σΘ®–ΓΘ©÷ΒΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣœρΝΩ![]() Θ§
Θ§![]() Θ§Κ· ΐ
Θ§Κ· ΐ![]() ΒΡΉν¥σ÷ΒΈΣ
ΒΡΉν¥σ÷ΒΈΣ![]() .
.
(1)«σ![]() ΒΡ¥σ–ΓΘΜ
ΒΡ¥σ–ΓΘΜ
(2)ΫΪΚ· ΐ![]() ΒΡΆΦœσœρΉσΤΫ“Τ
ΒΡΆΦœσœρΉσΤΫ“Τ![]() ΗωΒΞΈΜΘ§‘ΌΫΪΥυΒΟΆΦœσ…œΗςΒψΒΡΚαΉχ±ξΥθΕΧΈΣ‘≠ά¥ΒΡ
ΗωΒΞΈΜΘ§‘ΌΫΪΥυΒΟΆΦœσ…œΗςΒψΒΡΚαΉχ±ξΥθΕΧΈΣ‘≠ά¥ΒΡ![]() Θ§ΉίΉχ±ξ≤Μ±δΘ§ΒΟΒΫΚ· ΐ
Θ§ΉίΉχ±ξ≤Μ±δΘ§ΒΟΒΫΚ· ΐ![]() ΒΡΆΦœσΘ§Ής≥ωΚ· ΐ
ΒΡΆΦœσΘ§Ής≥ωΚ· ΐ![]() ‘Ύ
‘Ύ![]() ΒΡΆΦœσΘ°
ΒΡΆΦœσΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐfΘ®xΘ©=cos2x+2 ![]() sinxcosx©¹sin2xΘ°
sinxcosx©¹sin2xΘ°
Θ®1Θ©«σfΘ®xΘ©ΒΡΉν–Γ’ΐ÷ήΤΎΚΆ÷Β”ρΘΜ
Θ®2Θ©‘ΎΓςABC÷–Θ§Ϋ«AΘ§BΘ§CΥυΕ‘ΒΡ±ΏΖ÷±π «aΘ§bΘ§cΘ§»τ ![]() «“a2=bcΘ§ ‘≈–ΕœΓςABCΒΡ–ΈΉ¥Θ°
«“a2=bcΘ§ ‘≈–ΕœΓςABCΒΡ–ΈΉ¥Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…ηάκ–Ρ¬ ΈΣ ![]() ΒΡΆ÷‘≤
ΒΡΆ÷‘≤![]() ΒΡΉσΓΔ”“ΫΙΒψΈΣ
ΒΡΉσΓΔ”“ΫΙΒψΈΣ![]() , ΒψP «E…œ“ΜΒψ,
, ΒψP «E…œ“ΜΒψ, ![]() ,
, ![]() ΡΎ«–‘≤ΒΡΑκΨΕΈΣ
ΡΎ«–‘≤ΒΡΑκΨΕΈΣ ![]() .
.
(1)«σEΒΡΖΫ≥Χ;
(2)ΨΊ–ΈABCDΒΡΝΫΕΞΒψCΓΔD‘Ύ÷±œΏ![]() …œΘ§AΓΔB‘ΎΆ÷‘≤E…œ,»τΨΊ–ΈABCDΒΡ÷ή≥ΛΈΣ
…œΘ§AΓΔB‘ΎΆ÷‘≤E…œ,»τΨΊ–ΈABCDΒΡ÷ή≥ΛΈΣ ![]() , «σ÷±œΏABΒΡΖΫ≥Χ.
, «σ÷±œΏABΒΡΖΫ≥Χ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΝΫΕ®Βψ![]() Θ§
Θ§ ![]() Θ§«ζœΏ
Θ§«ζœΏ![]() …œΒΡΕ·Βψ
…œΒΡΕ·Βψ![]() ¬ζΉψ
¬ζΉψ![]() Θ§÷±œΏ
Θ§÷±œΏ![]() ”κ«ζœΏ
”κ«ζœΏ![]() ΒΡΝμ“ΜΗωΫΜΒψΈΣ
ΒΡΝμ“ΜΗωΫΜΒψΈΣ![]() Θ°
Θ°
Θ®ΔώΘ©«σ«ζœΏ![]() ΒΡ±ξΉΦΖΫ≥ΧΘΜ
ΒΡ±ξΉΦΖΫ≥ΧΘΜ
Θ®ΔρΘ©…ηΒψ![]() Θ§»τ
Θ§»τ![]() Θ§«σ÷±œΏ
Θ§«σ÷±œΏ![]() ΒΡΖΫ≥ΧΘ°
ΒΡΖΫ≥ΧΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΦΌ…ηΙΊ”ΎΡ≥…η±ΗΒΡ Ι”ΟΡξœόxΘ®ΡξΘ©ΚΆΥυ÷ß≥ωΒΡΈ§–όΖ―”ΟyΘ®Άρ‘ΣΘ©”–»γœ¬ΒΡΆ≥ΦΤΉ ΝœΘΚ
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
Θ®1Θ©Μ≠≥ω…ΔΒψΆΦ≤Δ≈–Εœ «ΖώœΏ–‘œύΙΊΘΜ
Θ®2Θ©»γΙϊœΏ–‘œύΙΊΘ§«σœΏ–‘ΜΊΙιΖΫ≥ΧΘΜ
Θ®3Θ©ΙάΦΤ Ι”ΟΡξœόΈΣ10Ρξ ±Θ§Έ§–όΖ―”Ο «Εύ…ΌΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐfΘ®xΘ©=2x3+bx2+cxΘ§ΤδΒΦΚ· ΐy=fΓδΘ®xΘ©ΒΡΆΦœσΘ®»γΆΦΥυ ΨΘ©Ψ≠ΙΐΒψΘ®1Θ§0Θ©Θ§Θ®2Θ§0Θ©Θ° Θ®ΔώΘ©«σfΘ®xΘ©ΒΡΫβΈω ΫΘΜ
Θ®ΔρΘ©»τΖΫ≥ΧfΘ®xΘ©©¹m=0«Γ”–2ΗωΗυΘ§«σmΒΡ÷ΒΘ°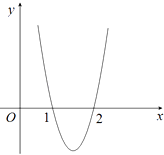
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§…ηOxΓΔOy «ΤΫΟφΡΎœύΫΜ≥…45ΓψΫ«ΒΡΝΫΧθ ΐ÷αΘ§ ![]() ΓΔ
ΓΔ ![]() Ζ÷±π «x÷αΓΔy÷α’ΐΖΫœρΆ§œρΒΡΒΞΈΜœρΝΩΘ§»τœρΝΩ
Ζ÷±π «x÷αΓΔy÷α’ΐΖΫœρΆ§œρΒΡΒΞΈΜœρΝΩΘ§»τœρΝΩ ![]() =x
=x ![]() +y
+y ![]() Θ§‘ρΑ―”––ρ ΐΕ‘Θ®xΘ§yΘ©Ϋ–ΉωœρΝΩ
Θ§‘ρΑ―”––ρ ΐΕ‘Θ®xΘ§yΘ©Ϋ–ΉωœρΝΩ ![]() ‘ΎΉχ±ξœΒxOy÷–ΒΡΉχ±ξΘ§‘Ύ¥ΥΉχ±ξœΒœ¬Θ§ΦΌ…η
‘ΎΉχ±ξœΒxOy÷–ΒΡΉχ±ξΘ§‘Ύ¥ΥΉχ±ξœΒœ¬Θ§ΦΌ…η ![]() =Θ®©¹2Θ§2
=Θ®©¹2Θ§2 ![]() Θ©Θ§
Θ©Θ§ ![]() =Θ®2Θ§0Θ©Θ§
=Θ®2Θ§0Θ©Θ§ ![]() =Θ®5Θ§©¹3
=Θ®5Θ§©¹3 ![]() Θ©Θ§‘ρœ¬Ν–ΟϋΧβ≤Μ’ΐ»ΖΒΡ «Θ® Θ©
Θ©Θ§‘ρœ¬Ν–ΟϋΧβ≤Μ’ΐ»ΖΒΡ «Θ® Θ© 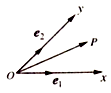
A.![]() =Θ®1Θ§0Θ©
=Θ®1Θ§0Θ©
B.| ![]() |=2
|=2 ![]()
C.![]() ΓΈ
ΓΈ ![]()
D.![]() ΓΆ
ΓΆ ![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
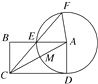
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΨΊ–ΈABCD÷–Θ§“‘AΈΣ‘≤–ΡΘ§ADΈΣΑκΨΕΒΡ‘≤ΫΜACΘ§AB”ΎMΘ§E.CEΒΡ―”≥ΛœΏΫΜΓ―A”ΎFΘ§CMΘΫ2Θ§ABΘΫ4.
(1)«σΓ―AΒΡΑκΨΕΘΜ
(2)«σCEΒΡ≥ΛΚΆΓςAFCΒΡΟφΜΐ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com