
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,对于任意
时,对于任意![]() ,总存在
,总存在![]() ,使得
,使得![]() ,求实数
,求实数![]() 的值.
的值.
【答案】(1)见解析;(2)3
【解析】
(1)分类讨论,求得函数的导数,利用导数与单调性的关系,即可求解;
(2)把对于任意![]() ,总存在
,总存在![]() ,使得
,使得![]() ,转化为
,转化为![]() ,结合函数的单调性,分类讨论,即可求解.
,结合函数的单调性,分类讨论,即可求解.
(1)由题意,函数![]() ,
,
当![]() 时,
时,![]() ,则
,则![]()
由![]() ,则
,则![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,则
,则![]() ,
,
由![]() ,令
,令![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() ,
,
令![]() ,即
,即![]() ,解得
,解得![]() ,
,
当![]() 时,即
时,即![]() 时,
时,
函数![]() 的单调递减区间为
的单调递减区间为![]() ,单调单调区间为
,单调单调区间为![]() ;
;
当![]() 时,即
时,即![]() ,
,
函数![]() 的单调递减区间为
的单调递减区间为 ,单调递增区间为
,单调递增区间为![]() .
.
(2)由对于任意![]() ,总存在
,总存在![]() ,使得
,使得![]() ,
,
等价于![]() ,
,
由(1)得,当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() ;
;
当![]() 时,
时,![]() 在
在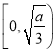 上单调递减,在
上单调递减,在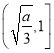 上单调递增,
上单调递增,
所以![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() ,得
,得![]() (舍去);
(舍去);
当![]() 时,
时,![]() ,则
,则![]() ,即
,即![]() ,
,
其中![]() ,而
,而![]() ,所以无解,舍去.
,所以无解,舍去.
综上所述,![]() .
.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:
【题目】新中国昂首阔步地走进2019年,迎来了她70岁华诞.某平台组织了“伟大的复兴之路一新中国70周年知识问答”活动,规则如下:共有30道单选题,每题4个选项中只有一个正确,每答对一题获得5颗红星,每答错一题反扣2颗红星;若放弃此题,则红星数无变化.答题所获得的红星可用来兑换神秘礼品,红星数越多奖品等级越高.小强参加该活动,其中有些题目会做,有些题目可以排除若干错误选项,其余的题目则完全不会.
(1)请问:对于完全不会的题目,小强应该随机从4个选项中选一个作答,还是选择放弃?(利用统计知识说明理由)
(2)若小强有12道题目会做,剩下的题目中,可以排除一个错误选项、可以排除两个错误选项和完全不会的题目的数量比是![]() .请问:小强在本次活动中可以获得最多红星数的期望是多少?
.请问:小强在本次活动中可以获得最多红星数的期望是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年春季,某出租汽车公司决定更换一批新的小汽车以代替原来报废的出租车,现有![]() 两款车型,根据以往这两种出租车车型的数据,得到两款出租车车型使用寿命频数表如下:
两款车型,根据以往这两种出租车车型的数据,得到两款出租车车型使用寿命频数表如下:
使用寿命年数 | 5年 | 6年 | 7年 | 8年 | 总计 |
| 10 | 20 | 45 | 25 | 100 |
| 15 | 35 | 40 | 10 | 100 |
(1)填写下表,并判断是否有![]() 的把握认为出租车的使用寿命年数与汽车车型有关?
的把握认为出租车的使用寿命年数与汽车车型有关?
使用寿命不高于 | 使用寿命不低于 | 总计 | |
| |||
| |||
总计 |
(2)司机师傅小李准备在一辆开了![]() 年的
年的![]() 型车和一辆开了
型车和一辆开了![]() 年的
年的![]() 型车中选择,为了尽最大可能实现
型车中选择,为了尽最大可能实现![]() 年内(含
年内(含![]() 年)不换车,试通过计算说明,他应如何选择.
年)不换车,试通过计算说明,他应如何选择.
附: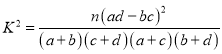 ,
,![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形![]() 为平行四边形,
为平行四边形,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() 是
是![]() 的中点.
的中点.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 与
与![]() 所成的角为
所成的角为![]() ? 若存在,求出
? 若存在,求出![]() 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() 与动直线
与动直线![]() 的交点为
的交点为![]() ,线段
,线段![]() 的中垂线与动直线
的中垂线与动直线![]() 的交点为
的交点为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过动点![]() 作曲线
作曲线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,
, ![]() ,求证:
,求证: ![]() 的大小为定值.
的大小为定值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)求不等式![]() 的解集;
的解集;
(2)若函数![]() 有两个极值点
有两个极值点![]() ,
,![]() (
(![]() )(若
)(若![]() 是函数
是函数![]() 的极大值或极小值,则m为函数
的极大值或极小值,则m为函数![]() 的极值点,极大值点与极小值点统称为极值点).
的极值点,极大值点与极小值点统称为极值点).
①求a的取值范围;
②证明:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com