
【题目】在正四棱柱![]() 中,E为AD的中点.
中,E为AD的中点.
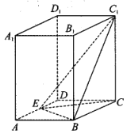
(1)在线段![]() 上是否存在点F,使得平面
上是否存在点F,使得平面![]() 平面
平面![]() ?并说明理由;
?并说明理由;
(2)设![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)存在,详见解析(2)![]()
【解析】
(1)找到![]() 的中点F,分别证出
的中点F,分别证出![]() 平面
平面![]() 与
与![]() 平面
平面![]() ,即可证明平面
,即可证明平面![]() 平面
平面![]() ﹔
﹔
(2)以D为坐标原点,DA,DC,![]() 所在直线分别为x轴、y轴、z轴建立空间直角坐标系,写出B,E,C,
所在直线分别为x轴、y轴、z轴建立空间直角坐标系,写出B,E,C,![]() 点的坐标,再分别求出平面
点的坐标,再分别求出平面![]() 与平面
与平面![]() 的法向量,利用空间向量的夹角公式求出二面角
的法向量,利用空间向量的夹角公式求出二面角![]() 的余弦值.
的余弦值.
解:(1)存在,当F为![]() 的中点时,平面
的中点时,平面![]() 平面
平面![]() .
.
因为![]() 为正四棱柱,
为正四棱柱,
所以![]() ,
,![]() .
.
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又因为E为AD的中点,F为![]() 的中点,
的中点,
所以![]() 且
且![]() .
.
连接AF,故四边形![]() 为平行四边形,
为平行四边形,
所以![]() .
.
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又因为![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
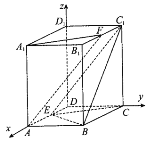
(2)以D为坐标原点,DA,DC,![]() 所在直线分别为x轴、y轴、z轴建立空间直角坐标系,如图所示.
所在直线分别为x轴、y轴、z轴建立空间直角坐标系,如图所示.
又因为![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则 ,即
,即![]() .
.
令![]() ,解得
,解得![]() ,
,
所以![]() ,
,
同理可求得平面![]() 的一个法向量为
的一个法向量为![]() .
.
所以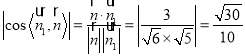 .
.
所以二面角![]() 的余弦值为
的余弦值为![]() ﹒
﹒


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
【题目】设函数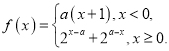 给出下列四个结论:①对
给出下列四个结论:①对![]() ,
,![]() ,使得
,使得![]() 无解;②对
无解;②对![]() ,
,![]() ,使得
,使得![]() 有两解;③当
有两解;③当![]() 时,
时,![]() ,使得
,使得![]() 有解;④当
有解;④当![]() 时,
时,![]() ,使得
,使得![]() 有三解.其中,所有正确结论的序号是______.
有三解.其中,所有正确结论的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代《九章算术》中将上,下两面为平行矩形的六面体称为刍童.如图的刍童![]() 有外接球,且
有外接球,且![]() ,
,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 与平面
与平面![]() 间的距离为
间的距离为![]() ,则该刍童外接球的体积为( )
,则该刍童外接球的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
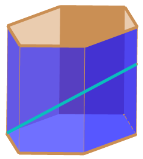
【题目】在我国瓷器的历史上六棱形的瓷器非常常见,因为六、八是中国人的吉利数字,所以好多瓷器都做成六棱形和八棱形.数学李老师有一个正六棱柱形状的笔筒,如图,底面边长为![]() ,高为
,高为![]() (底部及筒壁厚度忽略不计).一根长度为
(底部及筒壁厚度忽略不计).一根长度为![]() 的圆铁棒
的圆铁棒![]() (粗细忽略不计)斜放在笔筒内部,
(粗细忽略不计)斜放在笔筒内部,![]() 的一端置于正六棱柱某一侧棱的底端,另一端置于和该侧棱正对的侧棱上.一位小朋友玩耍时,向笔筒内注水,恰好将圆铁棒淹没,又将一个圆球放在笔筒口,球面又恰好接触水面,则球的表面积为______
的一端置于正六棱柱某一侧棱的底端,另一端置于和该侧棱正对的侧棱上.一位小朋友玩耍时,向笔筒内注水,恰好将圆铁棒淹没,又将一个圆球放在笔筒口,球面又恰好接触水面,则球的表面积为______![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
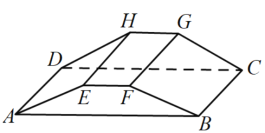
【题目】(本小题满分12分)如图,在多面体![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的的菱形,
的的菱形, ![]() ,四边形
,四边形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 和
和![]() 分别是
分别是![]() 和
和![]() 的中点.
的中点.

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com