
【题目】秉承提升学生核心素养的理念,学校开设以提升学生跨文化素养为核心的多元文化融合课程.选某艺术课程的学生唱歌、跳舞至少会一项,已知会唱歌的有![]() 人,会跳舞的有
人,会跳舞的有![]() 人,现从中选
人,现从中选![]() 人,设
人,设![]() 为选出的人中既会唱歌又会跳舞的人数,且
为选出的人中既会唱歌又会跳舞的人数,且![]()
(1)求选该艺术课程的学生人数;
(2)写出![]() 的概率分布列并计算
的概率分布列并计算![]() .
.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】新高考方案规定,普通高中学业水平考试分为合格性考试(合格考)和选择性考试(选择考).其中“选择考”成绩将计入高考总成绩,即“选择考”成绩根据学生考试时的原始卷面分数,由高到低进行排序,评定为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五个等级.某试点高中2018年参加“选择考”总人数是2016年参加“选择考”总人数的2倍,为了更好地分析该校学生“选择考”的水平情况,统计了该校2016年和2018年“选择考”成绩等级结果,得到如下图表:
五个等级.某试点高中2018年参加“选择考”总人数是2016年参加“选择考”总人数的2倍,为了更好地分析该校学生“选择考”的水平情况,统计了该校2016年和2018年“选择考”成绩等级结果,得到如下图表:
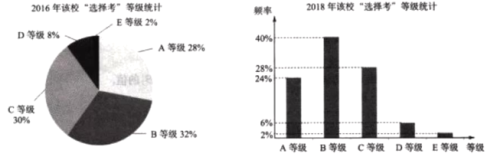
针对该校“选择考”情况,2018年与2016年比较,下列说法正确的是( )
A. 获得A等级的人数减少了B. 获得B等级的人数增加了1.5倍
C. 获得D等级的人数减少了一半D. 获得E等级的人数相同
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为a,∠D=60°,点H为DC边中点,现以线段AH为折痕将△DAH折起使得点D到达点P的位置且平面PHA⊥平面ABCH,点E,F分别为AB,AP的中点.

(1)求证:平面PBC∥平面EFH;
(2)若三棱锥P﹣EFH的体积等于![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】瑞士著名数学家欧拉在研究几何时曾定义欧拉三角形,![]() 的三个欧拉点(顶点与垂心连线的中点)构成的三角形称为
的三个欧拉点(顶点与垂心连线的中点)构成的三角形称为![]() 的欧拉三角形.如图,
的欧拉三角形.如图,![]() 是
是![]() 的欧拉三角形(H为
的欧拉三角形(H为![]() 的垂心).已知
的垂心).已知![]() ,
,![]() ,
,![]() ,若在
,若在![]() 内部随机选取一点,则此点取自阴影部分的概率为________.
内部随机选取一点,则此点取自阴影部分的概率为________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的短轴长为2,以椭圆
的短轴长为2,以椭圆![]() 的长轴为直径的圆与直线
的长轴为直径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() ,若直线
,若直线![]() 上存在点
上存在点![]() ,使得
,使得![]() 是以
是以![]() 为顶角的等腰直角三角形,求直线
为顶角的等腰直角三角形,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读如图判断闰年的流程图,判断公元1900年、公元2000年、公元2018年、公元2020年这四年中闰年的个数为(nMODm为n除以m的余数)( )
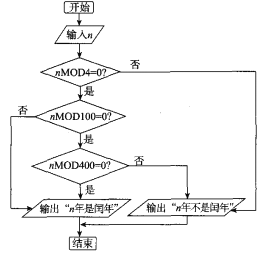
A.1个B.2个
C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com