
【题目】已知![]() .
.
(1)当![]() 时,求证:
时,求证:![]() ;
;
(2)若![]() 有三个零点时,求
有三个零点时,求![]() 的范围.
的范围.
【答案】(1)证明见解析;(2)![]() .
.
【解析】分析:(1)令![]() ,
,![]() ,
,![]() ,利用导数可得
,利用导数可得![]() 在
在![]() 上单调递减,
上单调递减,![]() ,从而可得结论; (2)
,从而可得结论; (2)![]() 有三个零点等价于
有三个零点等价于![]() 有三个零点,当
有三个零点,当![]() 时,当
时,当![]() 时,可得
时,可得![]() 是单调函数,至多有一个零点,不符合题意,当
是单调函数,至多有一个零点,不符合题意,当![]() 时,利用导数研究函数的单调性,根据单调性,结合函数图象可得
时,利用导数研究函数的单调性,根据单调性,结合函数图象可得![]() 的范围是
的范围是![]() .
.
详解:(1)证明: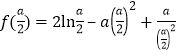 ,
,
令![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() 在
在![]() 上单调递减,
上单调递减,![]() ,
,
所以原命题成立.
(2)由![]()
![]() 有三个零点可得
有三个零点可得
![]() 有三个零点,
有三个零点,
![]() ,
,
①当![]() 时,
时,![]() 恒成立,可得
恒成立,可得![]() 至多有一个零点,不符合题意;
至多有一个零点,不符合题意;
②当![]() 时,
时,![]() 恒成立,可得
恒成立,可得![]() 至多有一个零点,不符合题意;
至多有一个零点,不符合题意;
③当![]() 时,记
时,记![]() 得两个零点为
得两个零点为![]() ,
,![]() ,不妨设
,不妨设![]() ,且
,且![]() ,
,
![]() 时,
时,![]() ;
;![]() 时,
时,![]() ;
;![]() 时
时![]() ,
,
观察可得![]() ,且
,且![]() ,
,
当![]() 时,
时,![]() ;
;![]() 单调递增,
单调递增,
所以有![]() ,即
,即![]() ,
,
![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
![]() 时
时![]() ,
,![]() 单调递减,
单调递减,
由(1)知,![]() ,且
,且![]() ,所以
,所以![]() 在
在![]() 上有一个零点,
上有一个零点,
由![]() ,且
,且![]() ,所以
,所以![]() 在
在![]() 上有一个零点,
上有一个零点,
综上可知![]() 有三个零点,
有三个零点,
即![]() 有三个零点,
有三个零点,
所求![]() 的范围是
的范围是![]() .
.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案科目:高中数学 来源: 题型:
【题目】为了解某养殖产品在某段时间内的生长情况,在该批产品中随机抽取了120件样本,测量其增长长度(单位:![]() ),经统计其增长长度均在区间
),经统计其增长长度均在区间![]() 内,将其按
内,将其按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6组,制成频率分布直方图,如图所示其中增长长度为
分成6组,制成频率分布直方图,如图所示其中增长长度为![]() 及以上的产品为优质产品.
及以上的产品为优质产品.

(1)求图中![]() 的值;
的值;
(2)已知这120件产品来自于![]() ,B两个试验区,部分数据如下列联表:
,B两个试验区,部分数据如下列联表:

将联表补充完整,并判断是否有99.99%的把握认为优质产品与A,B两个试验区有关系,并说明理由;
下面的临界值表仅供参考:

(参考公式: ,其中
,其中![]() )
)
(3)以样本的频率代表产品的概率,从这批产品中随机抽取4件进行分析研究,计算抽取的这4件产品中含优质产品的件数![]() 的分布列和数学期望E(X).
的分布列和数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽调了![]() 人,他们月收入的频数分布及对“楼市限购令”赞成人数如下表.
人,他们月收入的频数分布及对“楼市限购令”赞成人数如下表.
月收入(单位百元) |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
赞成人数 |
|
|
|
|
|
|
(1)由以上统计数据填下面![]() 列联表,并问是否有
列联表,并问是否有![]() 的把握认为“月收入以
的把握认为“月收入以![]() 元为分界点对“楼市限购令”的态度有差异;
元为分界点对“楼市限购令”的态度有差异;
月收入不低于 | 月收入低于 | 合计 | |
赞成 |
|
| ______________ |
不赞成 |
|
| ______________ |
合计 | ______________ | ______________ | ______________ |
(2)若对在![]() 、
、![]() 的被调查者中各随机选取两人进行追踪调查,记选中的
的被调查者中各随机选取两人进行追踪调查,记选中的![]() 人中不赞成“楼市限购令”的人数为
人中不赞成“楼市限购令”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式: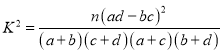 ,其中
,其中![]() .
.
参考值表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 在
在![]() 上的单调递增区间;
上的单调递增区间;
(2)将函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度,再将图象上所有点的横坐标伸长到原来的
个单位长度,再将图象上所有点的横坐标伸长到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象.求证:存在无穷多个互不相同的整数
的图象.求证:存在无穷多个互不相同的整数![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】密码学是一种密写技术,即把信息写成代码的技术,将信息转换成保密语言的过程叫编码,有保密形式语言道出原始信息的过程称作译码.凯撒(![]() 公元前100-前44年)曾使用过一种密码系统,现称为凯撒暗码,按照这种系统的规则,原始信息的字母都用另一字母代替,后者在标准字母表中的位置比前者靠后三位(即暗码
公元前100-前44年)曾使用过一种密码系统,现称为凯撒暗码,按照这种系统的规则,原始信息的字母都用另一字母代替,后者在标准字母表中的位置比前者靠后三位(即暗码![]() 原码后移3个位置).如:标准字母表:
原码后移3个位置).如:标准字母表:![]() ,凯撒暗码表:
,凯撒暗码表:![]() ,这样就将信息“JuliusCaesar”编码为“MxolxvFdhvdu”当你知道所得到的信息使用凯撒暗码编写成的密码时,译码工作很容易,只需把上述过程倒过来进行.当然现在的密写技术要复杂许多,这里我构造一种编码技术,请同学根据编码过程自己破译一下:信息字母与编码后暗语字母的对应法则是:暗码
,这样就将信息“JuliusCaesar”编码为“MxolxvFdhvdu”当你知道所得到的信息使用凯撒暗码编写成的密码时,译码工作很容易,只需把上述过程倒过来进行.当然现在的密写技术要复杂许多,这里我构造一种编码技术,请同学根据编码过程自己破译一下:信息字母与编码后暗语字母的对应法则是:暗码![]() 原码后移
原码后移![]() 后得到的字母(
后得到的字母(![]() 为原码字母在语句中的位置即第几个字母,若移出字母表则在后面续一张字母表,其中[]为取整符号,空格不计数).那么若一句话的暗码为“JnrzjPKNI”,其原码是__________.
为原码字母在语句中的位置即第几个字母,若移出字母表则在后面续一张字母表,其中[]为取整符号,空格不计数).那么若一句话的暗码为“JnrzjPKNI”,其原码是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com