
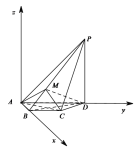
【题目】四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
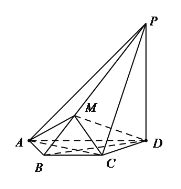
(1)求证: 平面![]() 平面
平面![]() ;
;
(2)![]() 为棱
为棱![]() 上异于
上异于![]() 的点,且
的点,且![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)根据相似三角形,证得![]() ,又由
,又由![]() 平面
平面![]() ,得到
,得到![]()
![]() ,利用线面垂直的判定定理,证得
,利用线面垂直的判定定理,证得![]() 平面
平面![]() ,再由面面垂直的判定定理,即可得到平面
,再由面面垂直的判定定理,即可得到平面![]() 平面
平面![]() .
.
(2)以![]() 为原点,
为原点,![]() 所在的直线为
所在的直线为![]() 轴,建立空间直角坐标系,设
轴,建立空间直角坐标系,设![]() ,
,![]() ,利用以
,利用以![]() ,求得
,求得![]() ,得到
,得到![]() ,再求得平面
,再求得平面![]() 的一个法向量
的一个法向量![]() ,利用向量的夹角公式,即可求解.
,利用向量的夹角公式,即可求解.
(1)证明:在![]() 与
与![]() 中,因为
中,因为![]() ,
, ![]() ,
,
所以![]() ,
,![]() ,即
,即![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() ,所以
,所以![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]()
![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() , 所以平面
, 所以平面![]() 平面
平面![]() .
.

(2)过![]() 作
作![]() ,因为
,因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,即
,即![]() 两两相垂直,以
两两相垂直,以![]() 为原点,
为原点,![]() 所在的直线为
所在的直线为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
因为![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设![]() ,
,![]() .则
.则![]() ,
,
![]() .
.
因为![]() ,所以
,所以![]() ,即
,即![]() ,
,
解得![]() ,
,![]() 或
或![]() .因为
.因为![]() ,所以
,所以![]() .
.
所以![]() ,即
,即![]() .
.
设![]() 为平面
为平面![]() 的一个法向量,则
的一个法向量,则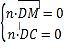 ,
,![]()
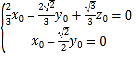
所以取![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
![]()
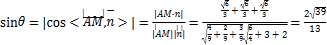 ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值
所成角的正弦值![]() .
.


科目:高中数学 来源: 题型:
【题目】某芯片公司对今年新开发的一批 5G 手机芯片进行测评,该公司随机调查了 100 颗芯片,所调查的芯片得分均在7,19内,将所得统计数据分为如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() 六个小组,得到如图所示的频率分布直方图,其中
六个小组,得到如图所示的频率分布直方图,其中![]() .
.
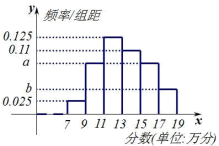
(1)求这 100 颗芯片评测分数的平均数;
(2)芯片公司另选 100 颗芯片交付给某手机公司进行测试,该手机公司将每颗芯片分别装在 3 个工程手机中进行初测若 3 个工程手机的评分都达到 13 万分,则认定该芯片合格;若 3 个工程手机中只要有 2 个评分没达到 13 万分,则认定该芯片不合格;若 3 个工程手机中仅 1 个评分没有达到 13万分,则将该芯片再分别置于另外 2 个工程手机中进行二测,二测时,2 个工程手机的评分都达到 13万分,则认定该芯片合格;2个工程手机中只要有 1 个评分没达到 13 万分,手机公司将认定该芯片不合格.已知每颗芯片在各次置于工程手机中的得分相互独立,并且芯片公司对芯片的评分方法及标准与手机公司对芯片的评分方法及标准都一致(以频率作为概率).每颗芯片置于一个工程手机中的测试费用均为 160 元,每颗芯片若被认定为合格或不合格,将不再进行后续测试.现手机公司测试部门预算的测试经费为 5 万元,试问预算经费是否足够测试完这 100 颗芯片?请说明理由.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在信息时代的今天,随着手机的发展,“微信”越来越成为人们交流的一种方法,某机构对“使用微信交流”的态度进行调查,随机抽取了100人,他们年龄的频数分布及对“使用微信交流”赞成的人数如下表:(注:年龄单位:岁)
年龄 |
|
|
|
|
|
|
频数 | 10 | 30 | 30 | 20 | 5 | 5 |
赞成人数 | 9 | 25 | 24 | 9 | 2 | 1 |
(1)若以“年龄45岁为分界点”,由以上统计数据完成下面的![]() 列联表,并通过计算判断是否在犯错误的概率不超过0.001的前提下认为“使用微信交流的态度与人的年龄有关”?
列联表,并通过计算判断是否在犯错误的概率不超过0.001的前提下认为“使用微信交流的态度与人的年龄有关”?
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(2)若从年龄在![]() ,
,![]() 调查的人中各随机选取1人进行追踪调查,求选中的2人中赞成“使用微信交流”的人数恰好为1人的概率.
调查的人中各随机选取1人进行追踪调查,求选中的2人中赞成“使用微信交流”的人数恰好为1人的概率.
| 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直角三角形ABC的三个顶点都在椭圆![]() 上,其中A(0,1)为直角顶点.若该三角形的面积的最大值为
上,其中A(0,1)为直角顶点.若该三角形的面积的最大值为![]() ,则实数a的值为_____.
,则实数a的值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com