
【题目】从万州二中高二年级文科学生中随机抽取60名学生,将其月考的政治成绩(均为整数)分成六段:![]() 后得到如下频率分布直方图.
后得到如下频率分布直方图.
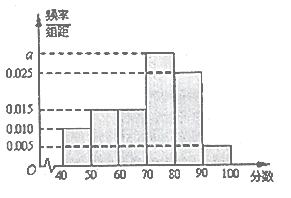
(1)求分数在![]() 内的频率;
内的频率;
(2)用分层抽样的方法在80分以上(含 80分)的学生中抽取一个容量为6的样本, 从该样本中任意选取2人,求其中恰有1 人的分数不低于90分的概率.
【答案】(1)0.3(2)![]()
【解析】分析:(1)利用频率分布直方图的矩形面积之和为![]() ,能求出分数在
,能求出分数在![]() 内的频率;(2)根据分层抽样方法可得,
内的频率;(2)根据分层抽样方法可得,![]() 分数段抽取的人数,
分数段抽取的人数,![]() 分数段抽取的人数,利用列举法求出
分数段抽取的人数,利用列举法求出![]() 人中任意选取
人中任意选取![]() 人共有
人共有![]() 种方法,其中恰有
种方法,其中恰有![]() 人的分数不低于90分的情况有
人的分数不低于90分的情况有![]() 种,利用古典概型概率公式可得结果.
种,利用古典概型概率公式可得结果.
详解: (Ⅰ)分数在![]() 内的频率为:
内的频率为:
![]()
(Ⅱ)由题意,![]() 分数段的人数为:
分数段的人数为:![]() 人
人
![]() 分数段的人数为:
分数段的人数为:![]() 人;
人;
∵用分层抽样的方法在80分以上(含80分)的学生中抽取一个容量为6的样本,
∴![]() 分数段抽取5人,
分数段抽取5人,![]() 分数段抽取1人,
分数段抽取1人,
因为从样本中任取2人,其中恰有1人的分数不低于90分,则另一人的
分数一定是在![]() 分数段,所以只需在分数段
分数段,所以只需在分数段![]() 抽取的5人中确定1人.
抽取的5人中确定1人.
设“从样本中任取2人,其中恰有1人的分数不低于90分为”事件![]() ,
,
![]()
![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() :
: ![]() ,右顶点为
,右顶点为 ![]() ,离心率为
,离心率为 ![]() ,直线
,直线 ![]() :
: ![]() 与椭圆
与椭圆 ![]() 相交于不同的两点
相交于不同的两点 ![]() ,
, ![]() ,过
,过 ![]() 的中点
的中点 ![]() 作垂直于
作垂直于 ![]() 的直线
的直线 ![]() ,设
,设 ![]() 与椭圆
与椭圆 ![]() 相交于不同的两点
相交于不同的两点 ![]() ,
, ![]() ,且
,且 ![]() 的中点为
的中点为 ![]() .
.
(Ⅰ)求椭圆 ![]() 的方程;
的方程;
(Ⅱ)设原点 ![]() 到直线
到直线 ![]() 的距离为
的距离为 ![]() ,求
,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,点P(0, ![]() ),以原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
),以原点为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为 ![]() .直线l的参数方程为
.直线l的参数方程为 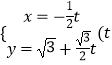 为参数).
为参数).
(Ⅰ)写出曲线C的直角坐标方程和直线l的普通方程;
(Ⅱ)设直线l与曲线C的两个交点分别为A,B,求 ![]() +
+ ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的实轴端点分别为A1 , A2 , 记双曲线的其中的一个焦点为F,一个虚轴端点为B,若在线段BF上(不含端点)有且仅有两个不同的点Pi(i=1,2),使得∠A1PiA2=
=1(a>0,b>0)的实轴端点分别为A1 , A2 , 记双曲线的其中的一个焦点为F,一个虚轴端点为B,若在线段BF上(不含端点)有且仅有两个不同的点Pi(i=1,2),使得∠A1PiA2= ![]() ,则双曲线的离心率e的取值范围是( )
,则双曲线的离心率e的取值范围是( )
A.( ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() )
)
C.(1, ![]() )
)
D.( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线的对称轴为坐标轴,顶点是坐标原点,准线方程为 ![]() ,直线
,直线 ![]() 与抛物线相交于不同的
与抛物线相交于不同的 ![]() ,
, ![]() 两点.
两点.
(1)求抛物线的标准方程;
(2)如果直线 ![]() 过抛物线的焦点,求
过抛物线的焦点,求 ![]() 的值;
的值;
(3)如果 ![]() ,直线
,直线 ![]() 是否过一定点,若过一定点,求出该定点;若不过一定点,试说明理由.
是否过一定点,若过一定点,求出该定点;若不过一定点,试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产一种仪器的元件,由于受生产能力和技术水平的限制,会产生一些次品,根据经验知道,其次品率P与日产量x(万件)之间大体满足关系:  (其中c为小于6的正常数). (注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品),已知每生产1万件合格的元件可以盈利2万元,但每生产出1万件次品将亏损1万元,故厂方希望定出合适的日产量.
(其中c为小于6的正常数). (注:次品率=次品数/生产量,如P=0.1表示每生产10件产品,有1件为次品,其余为合格品),已知每生产1万件合格的元件可以盈利2万元,但每生产出1万件次品将亏损1万元,故厂方希望定出合适的日产量.
(1)试将生产这种仪器的元件每天的盈利额T(万元)表示为日产量x(万件)的函数;
(2)当日产量为多少时,可获得最大利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com