
【题目】定义向量的外积:![]() 叫做向量
叫做向量![]() 与
与![]() 的外积,它是一个向量,满足下列两个条件:
的外积,它是一个向量,满足下列两个条件:
(1)![]() ,
,![]() ,且
,且![]() ,
,![]() 和
和![]() 构成右手系(即三个向量两两垂直,且三个向量的方向依次与拇指、食指、中指的指向一致);
构成右手系(即三个向量两两垂直,且三个向量的方向依次与拇指、食指、中指的指向一致);
(2)![]() 的模
的模![]() (
(![]() 表示向量
表示向量![]() 、
、![]() 的夹角);
的夹角);
如图,在正方体![]() ,有以下四个结论:
,有以下四个结论:
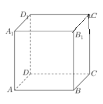
①![]() 与
与![]() 方向相反;
方向相反;
②![]() ;
;
③![]() 与正方体表面积的数值相等;
与正方体表面积的数值相等;
④![]() 与正方体体积的数值相等.
与正方体体积的数值相等.
这四个结论中,正确的结论有( )个
A.4B.3C.2D.1
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某数学小组到进行社会实践调查,了解到某公司为了实现1000万元利润目标,准备制定激励销售人员的奖励方案:在销售利润超过10万元时,按销售利润进行奖励,且奖金y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润的25%.同学们利用函数知识,设计了如下的函数模型,其中符合公司要求的是(参考数据:![]() ,
,![]() )( )
)( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,建立极坐标系,曲线
轴的非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为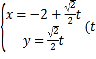 为参数
为参数![]() ,直线
,直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 两点.
两点.
(1)若点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值;
的值;
(2)求曲线![]() 的内接矩形周长的最大值.
的内接矩形周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的方程为
的方程为![]() ,其焦点为
,其焦点为![]() ,
,![]() 为过焦点
为过焦点![]() 的抛物线
的抛物线![]() 的弦,过
的弦,过![]() 分别作抛物线的切线
分别作抛物线的切线![]() ,
,![]() ,设
,设![]() ,
,![]() 相交于点
相交于点![]() .
.
(1)求![]() 的值;
的值;
(2)如果圆![]() 的方程为
的方程为![]() ,且点
,且点![]() 在圆
在圆![]() 内部,设直线
内部,设直线![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,说法正确的个数是( )
(1)若p![]() q为真命题,则p,q均为真命题
q为真命题,则p,q均为真命题
(2)命题“x0∈R,![]() 0”的否定是“x∈R,2x
0”的否定是“x∈R,2x![]() 0”
0”
(3)“![]() ”是“x∈[1,2],x2﹣
”是“x∈[1,2],x2﹣![]() 恒成立”的充分条件
恒成立”的充分条件
(4)在△ABC中,“![]() ”是“sinA>sinB”的必要不充分条件
”是“sinA>sinB”的必要不充分条件
(5)命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1”
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:![]() x∈R,ax2﹣2ax+1>0,命题q:指数函数f(x)=ax(a>0且a≠1)为减函数,则P是q的( )
x∈R,ax2﹣2ax+1>0,命题q:指数函数f(x)=ax(a>0且a≠1)为减函数,则P是q的( )
A.充分不必要条件B.必要不充分条件
C.充分必要条件D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为![]()
![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,取相同的长度单位建立极坐标系,曲线
轴的非负半轴为极轴,取相同的长度单位建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 上的点到直线l的最大距离为
上的点到直线l的最大距离为![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几个命题中,假命题是( )
A. “若![]() ,则
,则![]() ”的否命题
”的否命题
B. “![]() ,函数
,函数![]() 在定义域内单调递增”的否定
在定义域内单调递增”的否定
C. “![]() 是函数
是函数![]() 的一个周期”或“
的一个周期”或“![]() 是函数
是函数![]() 的一个周期”
的一个周期”
D. “![]() ”是“
”是“![]() ”的必要条件
”的必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com