练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    为了判断高中学生选读文科是否与性别有关，现随机抽取50名学生，得到如下2×2列联表：
    理科   文科    合计
           男     13    10     23
           女     7    20     27
          合计     20    30     50
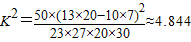    已知P（K2≥3.841）≈0.05，P（K2≥5.024）≈0.025，根据表中数据，得到，则在犯错误的概率不超过    的前提下可以认为选读文科与性别是有关系的．
    【答案】分析：根据条件中所给的观测值，同所给的临界值进行比较，根据4.844＞3.841，即可得到认为选修文科与性别有关系出错的可能性为5%．
    解答：解：∵根据表中数据，得到K2的观测值解，
    因为4.844＞3.841，
    ∴认为选修文科与性别有关系出错的可能性为5%．
    故答案为：5%．
    点评：本题考查独立性检验的应用，本题解题的关键是正确理解观测值对应的概率的意义．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    为了判断高中学生选读文科是否与性别有关，现随机抽取50名学生，得到如下2×2列联表：
    理科    文科     合计
           男      13     10      23
           女      7     20      27
          合计      20     30      50
    已知P（K2≥3.841）≈0.05，P（K2≥5.024）≈0.025，根据表中数据，得到K2=
    50×(13×20-10×7)2
    23×27×20×30
    ≈4.844    ，则在犯错误的概率不超过
    5%
    5%
    的前提下可以认为选读文科与性别是有关系的．

    查看答案和解析>>

    科目：高中数学 来源：2013届福建安溪一中、养正中学高二下期末联考理科数学试卷（解析版） 题型：填空题

    为了判断高中学生选读文科是否与性别有关，现随机抽取50名学生，得到如下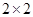列联表：

     

    理科

       文科 

        合计

           男

         13

        10

         23

           女

         7

        20

         27

          合计

         20

        30

         50

    已知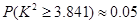,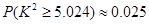，根据表中数据，得到

    ，则在犯错误的概率不超过           的前提下可以认为选读文科与性别是有关系的。

     

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    为了判断高中学生选读文科是否与性别有关，现随机抽取50名学生，得到如下2×2列联表：
    理科    文科     合计
           男      13     10      23
           女      7     20      27
          合计      20     30      50
    已知P（K2≥3.841）≈0.05，P（K2≥5.024）≈0.025，根据表中数据，得到K2=
    50×(13×20-10×7)2
    23×27×20×30
    ≈4.844    ，则在犯错误的概率不超过______的前提下可以认为选读文科与性别是有关系的．

    查看答案和解析>>

    同步练习册答案