
 =1(α为锐角)和圆(x-m)2+y2=r2相切于点A(4
=1(α为锐角)和圆(x-m)2+y2=r2相切于点A(4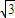 ,4),求α,m,r的值.
,4),求α,m,r的值.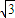 ,4)代入双曲线
,4)代入双曲线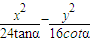 =1(α为锐角),求出α的值,联立双曲线和圆的方程,消去y得到关于x的一元二次方程,△=0,和把点A(4
=1(α为锐角),求出α的值,联立双曲线和圆的方程,消去y得到关于x的一元二次方程,△=0,和把点A(4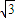 ,4)代入圆(x-m)2+y2=r2,解方程组即可求得m,r的值.
,4)代入圆(x-m)2+y2=r2,解方程组即可求得m,r的值.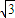 ,4)在双曲线上,
,4)在双曲线上,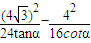 =1,
=1, -tanα=1
-tanα=1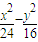 =1(1)
=1(1)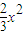 -16,
-16,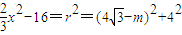 ,
, m-240=0.
m-240=0.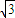 m+400=0,
m+400=0,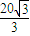 .
.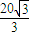 ,0),
,0),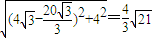 .
.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com