
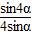 ,cosα•cos2α•cos4α=
,cosα•cos2α•cos4α= ,…,请你写出一个具有一般性的等式,使你写出的等式包含了已知等式(不要求证明),那么这个等式是: .
,…,请你写出一个具有一般性的等式,使你写出的等式包含了已知等式(不要求证明),那么这个等式是: .  课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| OM |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| c |
| a |
| b |
| c |
| π |
| 3 |
| a |
| c |
| a |
| c |
| b |
| c |
| a |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 6 |
| OM |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆C:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,过右焦点F且斜率为1的直线交椭圆C于A,B两点,N为弦AB的中点。
,过右焦点F且斜率为1的直线交椭圆C于A,B两点,N为弦AB的中点。
(1)求直线ON(O为坐标原点)的斜率KON ;
(2)对于椭圆C上任意一点M ,试证:总存在角![]() (
(![]() ∈R)使等式:
∈R)使等式:![]() =cos
=cos![]()
![]() +sin
+sin![]()
![]() 成立。w.w.w.k.s.5.u.c.o.m
成立。w.w.w.k.s.5.u.c.o.m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com