
【题目】已知函数f(x)= 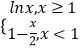 ,若F(x)=f[f(x)+1]+m有两个零点x1 , x2 , 则x1x2的取值范围是( )
,若F(x)=f[f(x)+1]+m有两个零点x1 , x2 , 则x1x2的取值范围是( )
A.[4﹣2ln2,+∞)
B.( ![]() ,+∞)
,+∞)
C.(﹣∞,4﹣2ln2]
D.(﹣∞, ![]() )
)
【答案】D
【解析】解:当x≥1时,f(x)=lnx≥0, ∴f(x)+1≥1,
∴f[f(x)+1]=ln(f(x)+1),
当x<1,f(x)=1﹣ ![]() >
> ![]() ,f(x)+1>
,f(x)+1> ![]() ,
,
f[f(x)+1]=ln(f(x)+1),
综上可知:F[f(x)+1]=ln(f(x)+1)+m=0,
则f(x)+1=e﹣m , f(x)=e﹣m﹣1,有两个根x1 , x2 , (不妨设x1<x2),
当x≥1是,lnx2=e﹣m﹣1,当x<1时,1﹣ ![]() =e﹣m﹣1,
=e﹣m﹣1,
令t=e﹣m﹣1> ![]() ,则lnx2=t,x2=et , 1﹣
,则lnx2=t,x2=et , 1﹣ ![]() =t,x1=2﹣2t,
=t,x1=2﹣2t,
∴x1x2=et(2﹣2t),t> ![]() ,
,
设g(t)=et(2﹣2t),t> ![]() ,
,
求导g′(t)=﹣2tet ,
t∈( ![]() ,+∞),g′(t)<0,函数g(t)单调递减,
,+∞),g′(t)<0,函数g(t)单调递减,
∴g(t)<g( ![]() )=
)= ![]() ,
,
∴g(x)的值域为(﹣∞, ![]() ),
),
∴x1x2取值范围为(﹣∞, ![]() ),
),
故选:D.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AC=1. 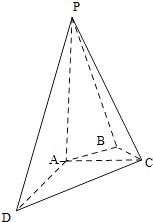
(1)证明:PC⊥AD;
(2)求二面角A﹣PC﹣D的正弦值;
(3)设E为棱PA上的点,满足异面直线BE与CD所成的角为30°,求AE的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
平面直角坐标系xOy中,曲线C:![]() .直线l经过点P(m,0),且倾斜角为
.直线l经过点P(m,0),且倾斜角为![]() .O为极点,以x轴正半轴为极轴,建立极坐标系.
.O为极点,以x轴正半轴为极轴,建立极坐标系.
(Ⅰ)写出曲线C的极坐标方程与直线l的参数方程;
(Ⅱ)若直线l与曲线C相交于A,B两点,且|PA|·|PB|=1,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面图形ABB1A1C1C如图4所示,其中BB1C1C是矩形,BC=2,BB1=4,AB=AC= ![]() ,A1B1=A1C1=
,A1B1=A1C1= ![]() .现将该平面图形分别沿BC和B1C1折叠,使△ABC与△A1B1C1所在平面都与平面BB1C1C垂直,再分别连接A2A,A2B,A2C,得到如图2所示的空间图形,对此空间图形解答下列问题.
.现将该平面图形分别沿BC和B1C1折叠,使△ABC与△A1B1C1所在平面都与平面BB1C1C垂直,再分别连接A2A,A2B,A2C,得到如图2所示的空间图形,对此空间图形解答下列问题.
(Ⅰ)证明:AA1⊥BC;
(Ⅱ)求AA1的长;
(Ⅲ)求二面角A﹣BC﹣A1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南宋时期的著名数学家秦九韶在他的著作《数学九章》中提出了秦九韶算法来计算多项式的值,在执行如图算法的程序框图时,若输入的n=5,x=2,则输出V的值为( ) 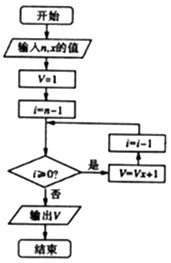
A.15
B.31
C.63
D.127
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且椭圆上的一点与两个焦点构成的三角形周长为
,且椭圆上的一点与两个焦点构成的三角形周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点.
两点.
①若线段![]() 中点的横坐标为
中点的横坐标为![]() ,求
,求![]() 的值;
的值;
②在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为定值?若是,求点
为定值?若是,求点![]() 的坐标;若不是,请说明理由.
的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子内装有8张卡片,每张卡片上面写着1个数字,这8个数字各不相同,且奇数有3个,偶数有5个.每张卡片被取出的概率相等.
(Ⅰ)如果从盒子中一次随机取出2张卡片,并且将取出的2张卡片上的数字相加得到一个新数,求所得新数是偶数的概率;
(Ⅱ)现从盒子中一次随机取出1张卡片,每次取出的卡片都不放回盒子,若取出的卡片上写着的数是偶数则停止取出卡片,否则继续取出卡片.设取出了![]() 次才停止取出卡片,求
次才停止取出卡片,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的最小值是1,且
的最小值是1,且![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)若![]() ,试求
,试求![]() 的最小值;
的最小值;
(3)若在区间![]() 上,
上,![]() 的图像恒在
的图像恒在![]() 的图像上方,试确定实数
的图像上方,试确定实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com