
【题目】已知二次函数![]() 的最小值是1,且
的最小值是1,且![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)若![]() ,试求
,试求![]() 的最小值;
的最小值;
(3)若在区间![]() 上,
上,![]() 的图像恒在
的图像恒在![]() 的图像上方,试确定实数
的图像上方,试确定实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ;(2)
;(2) 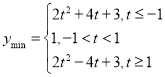 ; (3)
; (3) ![]()
【解析】
(1)设出二次函数![]() 的解析式,根据对称轴为
的解析式,根据对称轴为![]() ,
,![]() ,可以得到一个三元一次方程组,最后求出二次函数
,可以得到一个三元一次方程组,最后求出二次函数![]() 的解析式;
的解析式;
(2)根据对称轴和给定区间的位置关系进行分类讨论,然后根据二次函数的单调性,求出函数![]() 在
在![]() 时的最小值;
时的最小值;
(3)根据题意,原问题等价于![]() 在
在![]() 上恒成立,构造新函数,利用新函数的单调性,可以求出实数
上恒成立,构造新函数,利用新函数的单调性,可以求出实数![]() 的取值范围.
的取值范围.
(1)设二次函数![]() 的解析式为:
的解析式为:![]() ,因为
,因为![]() ,所以
,所以![]() 的对称轴为
的对称轴为![]() ,所以有
,所以有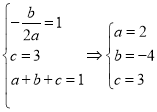 ,
,
因此函数![]() 的解析式为
的解析式为![]() ;
;
(2)若![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,![]() ;
;
若![]() ,即
,即![]() ,则
,则![]() 在
在![]() 上单调递减;
上单调递减;
![]() ;
;
若![]() ,即
,即![]() ,则
,则![]()
综上 .
.
(3)由题意知,当![]() 时,
时,![]() ,
,
即![]() 恒成立.
恒成立.
设![]() ,
,
因为当![]() 时,
时,![]() 单调递减,所以
单调递减,所以![]() ,
,
因此有![]() ,得
,得![]() ,即实数
,即实数![]() 的取值范围是
的取值范围是![]() .
.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= 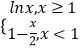 ,若F(x)=f[f(x)+1]+m有两个零点x1 , x2 , 则x1x2的取值范围是( )
,若F(x)=f[f(x)+1]+m有两个零点x1 , x2 , 则x1x2的取值范围是( )
A.[4﹣2ln2,+∞)
B.( ![]() ,+∞)
,+∞)
C.(﹣∞,4﹣2ln2]
D.(﹣∞, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() =1(a>0,b>0),过其左焦点F作x轴的垂线,交双曲线于A,B两点,若双曲线的右顶点在以AB为直径的圆外,则双曲线离心率的取值范围是( )
=1(a>0,b>0),过其左焦点F作x轴的垂线,交双曲线于A,B两点,若双曲线的右顶点在以AB为直径的圆外,则双曲线离心率的取值范围是( )
A.(1, ![]() )
)
B.(1,2)
C.( ![]() ,+∞)
,+∞)
D.(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,D,E分别是B1C1、BC的中点,∠BAC=90°,AB=AC=2,A1A=4,A1E= ![]() .
.
(Ⅰ)证明:A1D⊥平面A1BC;
(Ⅱ)求二面角A﹣BD﹣B1的平面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国传统文化中很多内容体现了数学的对称美,如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分展现了相互转化、对称统一的形式美、和谐美,给出定义:能够将圆O的周长和面积同时平分的函数称为这个圆的“优美函数”,给出下列命题:
①对于任意一个圆O,其“优美函数“有无数个”;
②函数 ![]() 可以是某个圆的“优美函数”;
可以是某个圆的“优美函数”;
③正弦函数y=sinx可以同时是无数个圆的“优美函数”;
④函数y=f(x)是“优美函数”的充要条件为函数y=f(x)的图象是中心对称图形.
其中正确的命题是( )
A.①③
B.①③④
C.②③
D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)判断函数的奇偶性,并加以证明;
(2)用定义证明![]() 在
在![]() 上是减函数;
上是减函数;
(3)函数![]() 在
在![]() 上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
上是单调增函数还是单调减函数?(直接写出答案,不要求写证明过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com