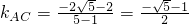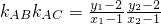A
分析:先讨论直线BC斜率不存在时,求出B,C的坐标,求出AB、AC斜率,求出k
AB•k
AC=-1,得到三角形ABC是直角三角形,当BC斜率存在时设出其方程,联立BC的方程与抛物线的方程,利用韦达定理,表示出AB、AC斜率,求出k
AB•k
AC=-1,得到三角形ABC是直角三角形.
解答:当BC斜率不存在时,方程为x=5,
代入抛物线方程y
2=4x得
B

,C
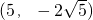
所以AB斜率是
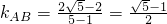
,
AC斜率是
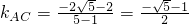
所以k
AB•k
AC=-1,
所以AB与AC垂直,
所以三角形ABC是直角三角形当BC斜率存在时,显然不能为0,否则与抛物线只有一个公共点,
所以设方程为x-5=a(y+2)(a是斜率的倒数),
代入抛物线方程化简得y
2-4ay-8a-20=0 设B(x
1,y
1),C(x
2,y
2),
则y
1+y
2=4a,y
1y
2=-8a-20 x
1+x
2=(ay
1+2a+5)+(ay
2+2a+5)=a(y
1+y
2)+4a+10=4a
2+4a+10 x
1x
2=(ay
1+2a+5)(ay
2+2a+5)=4a
2+20a+25
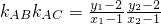
因为(y
1-2)(y
2-2)=y
1y
2-2(y
1+y
2)+4=-16a-16 (x
1-1)(x
2-1)=x
1x
2-(x
1+x
2)+1=16a+16 所以AB和AC斜率乘积等于-1,
即AB垂直于AC.综上可知,三角形ABC是直角三角形
故选A.
点评:解决直线与圆锥曲线的位置关系问题,一般讲直线的方程与圆锥曲线的方程联立,利用韦达定理找突破口.

 ,C
,C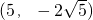
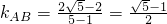 ,
,