
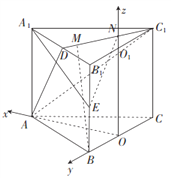
【题目】如图,在各棱长均为2的正三棱柱![]() 中,
中, ![]() 分别为棱
分别为棱![]() 与
与![]() 的中点,
的中点, ![]() 为线段
为线段![]() 上的动点,其中,
上的动点,其中, ![]() 更靠近
更靠近![]() ,且
,且![]() .
.

(1)证明: ![]() 平面
平面![]() ;
;
(2)若![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求异面直线
,求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1)证明见解析.
(2)![]() .
.
【解析】试题分析:(1)根据正三角形性质得![]() ,结合线面垂直得
,结合线面垂直得![]() .因此可得
.因此可得![]() 平面
平面![]() ,即
,即![]() .再根据
.再根据![]() ,得
,得![]() 平面
平面![]() ,(2)先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解平面
,(2)先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解平面![]() 法向量,根据向量数量积求夹角,再根据线面角与向量夹角互余关系列方程,解得N坐标,最后根据向量数量积求异面直线
法向量,根据向量数量积求夹角,再根据线面角与向量夹角互余关系列方程,解得N坐标,最后根据向量数量积求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
试题解析:解:(1)证明:由已知得![]() 为正三角形,
为正三角形,![]() 为棱
为棱![]() 的中点,
的中点,
∴![]() ,
,
在正三棱柱![]() 中,
中,![]() 底面
底面![]() ,则
,则![]() .
.
又![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]() .
.
易证![]() ,又
,又![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)解:取![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,则
,则![]() ,
,![]() ,
,
以![]() 为坐标原点,建立如图所示的空间直角坐标系
为坐标原点,建立如图所示的空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设![]()
![]() ,
,
则![]()
![]()
![]() ,
,
易知![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
∴![]()
![]()
![]() ,解得
,解得![]() .
.
∴![]() ,
,![]()
![]() ,
,![]()
![]() ,,
,,
∴![]()
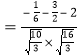
![]() ,
,
∴异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 在区间
在区间![]() 上有最小值1,最大值9.
上有最小值1,最大值9.
(1)求实数a,b的值;
(2)设![]() ,若不等式
,若不等式![]() 在区间
在区间![]() 上恒成立,求实数k的取值范围;
上恒成立,求实数k的取值范围;
(3)设![]() ),若函数
),若函数![]() 有三个零点,求实数
有三个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先阅读下列不等式的证法,再解决后面的问题:
已知![]() ,
,![]() ,求证:
,求证:![]() .
.
证明:构造函数![]() ,
,
即![]()
![]() .
.
因为对一切![]() ,恒有
,恒有![]() ,
,
所以![]() ,从而得
,从而得![]() .
.
(1)若![]() ,
,![]() ,请写出上述结论的推广式;
,请写出上述结论的推广式;
(2)参考上述证法,对你推广的结论加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中错误的是( )
A.先把高二年级的2000名学生编号:1到2000,再从编号为1到50的学生中随机抽取1名学生,其编号为![]() ,然后抽取编号为
,然后抽取编号为![]() ,
,![]() ,
,![]() ,……的学生,这种抽样方法是系统抽样法.
,……的学生,这种抽样方法是系统抽样法.
B.一组数据的方差为![]() ,平均数为
,平均数为![]() ,将这组数据的每一个数都乘以2,所得的一组新数据的方差和平均数为
,将这组数据的每一个数都乘以2,所得的一组新数据的方差和平均数为![]() ,
,![]() .
.
C.若两个随机变量的线性相关性越强,则相关系数![]() 的值越接近于1.
的值越接近于1.
D.若一组数据1,![]() ,3的平均数是2,则该组数据的方差是
,3的平均数是2,则该组数据的方差是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面上动点![]() 到点
到点![]() 的距离与到直线
的距离与到直线![]() 的距离之比为
的距离之比为![]() ,记动点
,记动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)设![]() 是曲线
是曲线![]() 上的动点,直线
上的动点,直线![]() 的方程为
的方程为![]() .
.
①设直线![]() 与圆
与圆![]() 交于不同两点
交于不同两点![]() ,
, ![]() ,求
,求![]() 的取值范围;
的取值范围;
②求与动直线![]() 恒相切的定椭圆
恒相切的定椭圆![]() 的方程;并探究:若
的方程;并探究:若![]() 是曲线
是曲线![]() :
: ![]() 上的动点,是否存在直线
上的动点,是否存在直线![]() :
: ![]() 恒相切的定曲线
恒相切的定曲线![]() ?若存在,直接写出曲线
?若存在,直接写出曲线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 是公差为2的等差数列,数列
是公差为2的等差数列,数列![]() 满足b1=1,b2=2,且anbn+bn=nbn+1.
满足b1=1,b2=2,且anbn+bn=nbn+1.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足
满足![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,若不等式
,若不等式![]()
对一切n∈N*恒成立,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场在促销期间规定:商场内所有商品按标价的![]() 出售,当顾客在商场内消费一定金额后,按如下方案获得相应金额的奖券:
出售,当顾客在商场内消费一定金额后,按如下方案获得相应金额的奖券:
消费金额(元)的范围 |
|
|
|
| … |
获得奖券的金额(元) | 30 | 60 | 100 | 130 | … |
根据上述促销方法,顾客在该商场购物可以获得双重优惠,例如:购买标价为400元的商品,则消费金额为320元,获得的优惠额为:![]() 元,设购买商品得到的优惠率=(购买商品获得的优惠额)/(商品标价),试问:
元,设购买商品得到的优惠率=(购买商品获得的优惠额)/(商品标价),试问:
(1)若购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)对于标价在![]() (元)内的商品,顾客购买标价为多少元的商品,可得到不小于
(元)内的商品,顾客购买标价为多少元的商品,可得到不小于![]() 的优惠率?
的优惠率?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com