
【题目】给定一个数列{an},在这个数列里,任取m(m≥3,m∈N*)项,并且不改变它们在数列{an}中的先后次序,得到的数列{an}的一个m阶子数列.
已知数列{an}的通项公式为an= ![]() (n∈N* , a为常数),等差数列a2 , a3 , a6是数列{an}的一个3子阶数列.
(n∈N* , a为常数),等差数列a2 , a3 , a6是数列{an}的一个3子阶数列.
(1)求a的值;
(2)等差数列b1 , b2 , …,bm是{an}的一个m(m≥3,m∈N*)阶子数列,且b1= ![]() (k为常数,k∈N* , k≥2),求证:m≤k+1
(k为常数,k∈N* , k≥2),求证:m≤k+1
(3)等比数列c1 , c2 , …,cm是{an}的一个m(m≥3,m∈N*)阶子数列,求证:c1+c1+…+cm≤2﹣ ![]() .
.
【答案】
(1)解:∵a2,a3,a6成等差数列,
∴a2﹣a3=a3﹣a6.
又∵a2= ![]() ,a3=
,a3= ![]() ,a6=
,a6= ![]() ,
,
代入得 ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() ,解得a=0
,解得a=0
(2)证明:设等差数列b1,b2,…,bm的公差为d.
∵b1= ![]() ,∴b2≤
,∴b2≤ ![]() ,
,
从而d=b2﹣b1≤ ![]() ﹣
﹣ ![]() =﹣
=﹣ ![]() .
.
∴bm=b1+(m﹣1)d≤ ![]() ﹣
﹣ ![]() .
.
又∵bm>0,∴ ![]() ﹣
﹣ ![]() >0.
>0.
即m﹣1<k+1.
∴m<k+2.
又∵m,k∈N*,∴m≤k+1.
(3)证明:设c1= ![]() (t∈N*),等比数列c1,c2,…,cm的公比为q.
(t∈N*),等比数列c1,c2,…,cm的公比为q.
∵c2≤ ![]() ,∴q=
,∴q= ![]() ≤
≤ ![]() .
.
从而cn=c1qn﹣1≤ ![]() (1≤n≤m,n∈N*).
(1≤n≤m,n∈N*).
∴c1+c2+…+cm≤ ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]()
= ![]() ,
,
设函数f(x)=x﹣ ![]() ,(m≥3,m∈N*).
,(m≥3,m∈N*).
当x∈(0,+∞)时,函数f(x)=x﹣ ![]() 为单调增函数.
为单调增函数.
∵当t∈N*,∴1< ![]() ≤2.∴f(
≤2.∴f( ![]() )≤2﹣
)≤2﹣ ![]() .
.
即 c1+c2+…+cm≤2﹣ ![]() .
.
【解析】(1)利用等差数列的定义及其性质即可得出;(2)设等差数列b1 , b2 , …,bm的公差为d.由b1= ![]() ,可得b2≤
,可得b2≤ ![]() ,再利用等差数列的通项公式及其不等式的性质即可证明;(3)设c1=
,再利用等差数列的通项公式及其不等式的性质即可证明;(3)设c1= ![]() (t∈N*),等比数列c1 , c2 , …,cm的公比为q.由c2≤
(t∈N*),等比数列c1 , c2 , …,cm的公比为q.由c2≤ ![]() ,可得q=
,可得q= ![]() ≤
≤ ![]() .从而cn=c1qn﹣1≤
.从而cn=c1qn﹣1≤ ![]() (1≤n≤m,n∈N*).再利用等比数列的前n项和公式、函数的单调性即可得出.
(1≤n≤m,n∈N*).再利用等比数列的前n项和公式、函数的单调性即可得出.
【考点精析】通过灵活运用数列的前n项和和等差数列的性质,掌握数列{an}的前n项和sn与通项an的关系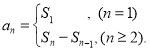 ;在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列即可以解答此题.
;在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知二次函数![]() ,则下列说法不正确的是( )
,则下列说法不正确的是( )
A.其图象开口向上,且始终与![]() 轴有两个不同的交点
轴有两个不同的交点
B.无论![]() 取何实数,其图象始终过定点
取何实数,其图象始终过定点![]()
C.其图象对称轴的位置没有确定,但其形状不会因![]() 的取值不同而改变
的取值不同而改变
D.函数的最小值大于![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将5名报名参加运动会的同学分别安排到跳绳、接力,投篮三项比赛中(假设这些比赛都不设人数上限),每人只参加一项,则共有![]() 种不同的方案;若每项比赛至少要安排一人时,则共有
种不同的方案;若每项比赛至少要安排一人时,则共有![]() 种不同的方案,其中
种不同的方案,其中![]() 的值为( )
的值为( )
A. 543 B. 425 C. 393 D. 275
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,E为PC中点,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=1,CD=2. 
(1)求证:BE∥平面PAD;
(2)求证:BC⊥平面PBD;
(3)在线段PC上是否存在一点Q,使得二面角Q﹣BD﹣P为45°?若存在,求 ![]() 的值;若不存在,请述明理由.
的值;若不存在,请述明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率
的离心率![]() ,该椭圆中心到直线
,该椭圆中心到直线![]() 的距离为
的距离为![]() .
.
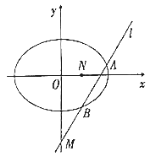
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在过点![]() 的直线
的直线![]() ,使直线
,使直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且以
两点,且以![]() 为直径的圆过定点
为直径的圆过定点![]() ?若存在,求出所有符合条件的直线方程;若不存在,请说明理由.
?若存在,求出所有符合条件的直线方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log4(ax2+2x+3).
(1)若f(1)=1,求f(x)的单调区间;
(2)是否存在实数a,使f(x)的最小值为0?若存在,求出a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=﹣ex+ex(e为自然对数的底数)
(1)求函数f(x)的最大值;
(2)设g(x)=lnx+ ![]() x2+ax,若对任意x1∈(0,2],总存在x2∈(0,2].使得g(x1)<f(x2),求实数a的取值范围.
x2+ax,若对任意x1∈(0,2],总存在x2∈(0,2].使得g(x1)<f(x2),求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖,某顾客从此10张券中任抽2张,求:
(1)该顾客中奖的概率;
(2)该顾客获得的奖品总价值X(元)的概率分布列和期望E(X).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com