
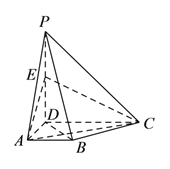
【题目】如图,在四棱锥![]() 中,
中, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为棱
为棱![]() 的中点.
的中点.
(![]() )求证:
)求证: ![]() .
.
(![]() )求证:平面
)求证:平面![]() 平面
平面![]() .
.
(![]() )试判断
)试判断![]() 与平面
与平面![]() 是否平行?并说明理由.
是否平行?并说明理由.
【答案】(1)见解析;(2)见解析(3)见解析.
【解析】试题分析:(1)PD⊥底面ABCD,DC底面ABCDPD⊥DC.又AD⊥DC,AD∩PD=D故CD⊥平面PAD.又AE平面PAD,得CD⊥AE.
(2)由AB∥DC,CD⊥平面PAD,AB⊥平面PAD.又由AB平面PAB,得平面PAB⊥平面PAD.
(3)PB与平面AEC不平行.假设PB∥平面AEC,由已知得到![]() ,这与
,这与![]() 矛盾.
矛盾.
试题解析:
(![]() )证明:∵
)证明:∵![]() 底面
底面![]() ,
, ![]() 底面
底面![]() ,
,
∴![]() ,
,
又![]() ,
, ![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() .
.
(![]() )证明:
)证明: ![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(![]() )
)![]() 与平面
与平面![]() 不平行,
不平行,
假设![]() 平面
平面![]() ,设
,设![]() ,
,
连结![]() ,则平面
,则平面![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
∴![]() ,
,
∴在![]() 中有
中有![]() ,
,
由![]() 是
是![]() 中点可得
中点可得![]() ,即
,即![]() ,
,
∵![]() ,
,
∴![]() ,这与
,这与![]() 矛盾,
矛盾,
所以假设不成立,即![]() 与平面
与平面![]() 不平行.
不平行.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
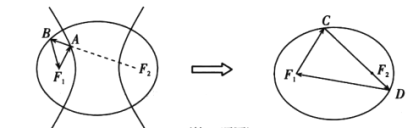
【题目】光线从椭圆的一个焦点发出,被椭圆反射后会经过椭圆的另一个焦点;光线从双曲线的一个焦点发出,被双曲线反射后的反射光线等效于从另一个焦点射出.如图,一个光学装置由有公共焦点![]() ,
,![]() 的椭圆
的椭圆![]() 与双曲线
与双曲线![]() 构成,现一光线从左焦点
构成,现一光线从左焦点![]() 发出,依次经
发出,依次经![]() 与
与![]() 反射,又回到了点
反射,又回到了点![]() ,历时
,历时![]() 秒;若将装置中的
秒;若将装置中的![]() 去掉,此光线从点
去掉,此光线从点![]() 发出,经
发出,经![]() 两次反射后又回到了点
两次反射后又回到了点![]() ,历时
,历时![]() 秒;若
秒;若![]() ,则
,则![]() 与
与![]() 的离心率之比为( )
的离心率之比为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①命题“x∈R,cosx>0”的否定是“x0∈R,cosx0≤0”;
②若0<a<1,则函数f(x)=x2+ax-3只有一个零点;
③函数y=2![]() sinxcosx在
sinxcosx在![]() 上是单调递减函数;
上是单调递减函数;
④若lga+lgb=lg(a+b),则a+b的最小值为4.
其中真命题的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公交车的数量太多容易造成资源浪费,太少又难以满足乘客的需求,为了合理布置车辆,公交公司在2路车的乘客中随机调查了50名乘客,经整理,他们候车时间(单位:![]() )的茎叶图如下:
)的茎叶图如下:

(Ⅰ)将候车时间分为![]() 八组,作出相应的频率分布直方图;
八组,作出相应的频率分布直方图;
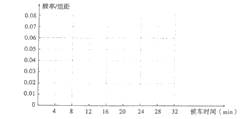
(Ⅱ)若公交公司将2路车发车时间调整为每隔15![]() 发一趟车,那么上述样本点将发生变化(例如候车时间为9
发一趟车,那么上述样本点将发生变化(例如候车时间为9![]() 的不变,候车时间为17
的不变,候车时间为17![]() 的变为2
的变为2![]() ),现从2路车的乘客中任取5人,设其中候车时间不超过10
),现从2路车的乘客中任取5人,设其中候车时间不超过10![]() 的乘客人数为
的乘客人数为![]() ,求
,求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() .过抛物线
.过抛物线![]() 上一点
上一点![]() 作
作![]() 的切线
的切线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点.
两点.
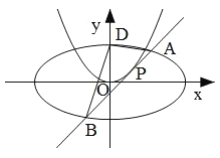
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)是否存在直线![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下给出五个命题,其中真命题的序号为______
①函数![]() 在区间
在区间![]() 上存在一个零点,则
上存在一个零点,则![]() 的取值范围是
的取值范围是![]() 或
或![]() ;
;
②“任意菱形的对角线一定相等”的否定是“菱形的对角线一定不相等”;
③![]() ,
,![]() ;
;
④若![]() ,则
,则![]() ;
;
⑤“![]() ”是“
”是“![]() 成等比数列”的充分不必要条件.
成等比数列”的充分不必要条件.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com