
【题目】已知 ![]() “直线
“直线 ![]() 与圆
与圆 ![]() 相交”;
相交”; ![]() :“方程
:“方程 ![]() 有一正根和一负根”.若
有一正根和一负根”.若 ![]() 或
或 ![]() 为真, 非p为真,求实数
为真, 非p为真,求实数 ![]() 的取值范围.
的取值范围.
【答案】解:对p:∵直线与圆相交,∴d= ![]() <1. ∴-
<1. ∴- ![]() +1<m<
+1<m< ![]() +1.
+1.
对q:方程mx2-x+m-4=0有一正根和一负根,
∴令f(x)=mx2-x+m-4,
∴ ![]() 或
或 ![]() 解得0<m<4.
解得0<m<4.
又∵p为真,∴p假. 又∵p或q为真,∴q为真.
由数轴可得 ![]() +1≤m<4.
+1≤m<4.
故m的取值范围是 ![]() +1≤m<4
+1≤m<4
【解析】本题主要考查复合命题的真假判断的应用。要根据已知条件先求出p或q为真命题,非p为真命题的等价条件,根据分析可得p为假命题,q为真命题,命题p和q的解题即可求出m的取值范围。
【考点精析】解答此题的关键在于理解复合命题的真假的相关知识,掌握“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PC⊥底面ABCD,AD∥BC,AD=2BC=2,PC=2,△ABC是以AC为斜边的等腰直角三角形,E是PD的中点.
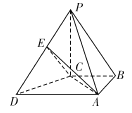
(1)求证:平面EAC⊥平面PCD;
(2)求直线PA与平面EAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,过对角线
中,过对角线![]() 的一个平面交
的一个平面交![]() 于点
于点![]() ,交
,交![]() 于
于![]() .
.
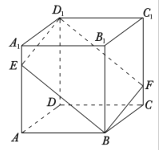
①四边形![]() 一定是平行四边形;
一定是平行四边形;
②四边形![]() 有可能是正方形;
有可能是正方形;
③四边形![]() 在底面
在底面![]() 内的投影一定是正方形;
内的投影一定是正方形;
④四边形![]() 有可能垂直于平面
有可能垂直于平面![]() .
.
以上结论正确的为_______________.(写出所有正确结论的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了及时向群众宣传“十九大”党和国家“乡村振兴”战略,需要寻找一个宣讲站,让群众能在最短的时间内到宣讲站.设有三个乡镇,分别位于一个矩形![]() 的两个顶点
的两个顶点![]() 及
及![]() 的中点
的中点![]() 处,
处,![]() ,
,![]() ,现要在该矩形的区域内(含边界),且与
,现要在该矩形的区域内(含边界),且与![]() 等距离的一点
等距离的一点![]() 处设一个宣讲站,记
处设一个宣讲站,记![]() 点到三个乡镇的距离之和为
点到三个乡镇的距离之和为![]() .
.
(Ⅰ)设![]() ,将
,将![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅱ)试利用(Ⅰ)的函数关系式确定宣讲站![]() 的位置,使宣讲站
的位置,使宣讲站![]() 到三个乡镇的距离之和
到三个乡镇的距离之和![]() 最小.
最小.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的实轴端点分别为A1 , A2 , 记双曲线的其中的一个焦点为F,一个虚轴端点为B,若在线段BF上(不含端点)有且仅有两个不同的点Pi(i=1,2),使得∠A1PiA2=
=1(a>0,b>0)的实轴端点分别为A1 , A2 , 记双曲线的其中的一个焦点为F,一个虚轴端点为B,若在线段BF上(不含端点)有且仅有两个不同的点Pi(i=1,2),使得∠A1PiA2= ![]() ,则双曲线的离心率e的取值范围是( )
,则双曲线的离心率e的取值范围是( )
A.( ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() )
)
C.(1, ![]() )
)
D.( ![]() ,+∞)
,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com