
【题目】设![]() 、
、![]() 、
、![]() 为集合
为集合![]() 的任意三个
的任意三个![]() 元子集,且
元子集,且![]() ,
,![]() .问:是否存在
.问:是否存在![]() ,
,![]() ,
,![]() ,使得其中某两个数的和等于第三个数?
,使得其中某两个数的和等于第三个数?
【答案】见解析
【解析】
用反证法证明:存在![]() ,
,![]() ,
,![]() ,使其中某两个数的和等于第三个数.
,使其中某两个数的和等于第三个数.
假设存在某种分拆,![]() ,
,![]() ,
,
使得![]() 、
、![]() 、
、![]() 三个
三个![]() 元集中不存在这样的三个元素.
元集中不存在这样的三个元素.
记![]() ,
,![]() ,
,![]() ,
,
其中,![]() ,
,![]() ,
,![]() .
.
设![]() ,则
,则![]() ,
,![]() ,而
,而![]() .
.
考虑集合![]() ,记
,记![]() .
.
则![]() 为正整数.
为正整数.
(1)若![]() ,则
,则![]() ,矛盾.
,矛盾.
(2)若![]() ,考虑
,考虑![]() 个数
个数![]() .
.
对每个![]() ,显然
,显然![]() .
.
又若存在某个![]() ,则
,则![]() 与
与![]() ,
,![]() ,
,![]() ,矛盾.
,矛盾.
于是,所有的![]() ,而
,而![]() ,
,
此时,集合![]() 中至少有
中至少有![]() 个元素
个元素![]() ,也得矛盾.
,也得矛盾.
(3)若![]() ,在数列
,在数列![]() 中,自左至右设最先取到
中,自左至右设最先取到![]() 的项为
的项为![]() .
.
考虑数![]() 与
与![]() ,其显然均在 集合
,其显然均在 集合![]() 中.
中.
由于![]() ,而
,而![]() 、
、![]() 分 别为集合
分 别为集合![]() 、
、![]() 的元素,故由假设知
的元素,故由假设知![]() .
.
又据![]() ,知
,知![]() ,而
,而![]() ,由假设知
,由假设知![]() .
.
因此,只有![]() .
.
再由![]() ,得
,得![]() ;由
;由![]() ,得
,得![]() .
.
因此,只有![]() .
.
由于集合![]() 中的两个元素
中的两个元素![]() 与
与![]() 的差为
的差为![]() ,
,
故它们为集合![]() 中相邻的两个元素,并且它们分别小于
中相邻的两个元素,并且它们分别小于![]() 及
及![]() .
.
因此,在集合![]() 中应当排在先前的一对 元素
中应当排在先前的一对 元素![]() 、
、![]() 之前,
之前,
这与![]() 、
、![]() 为集合
为集合![]() 中 最先使得其差为
中 最先使得其差为![]() 的项的假设矛盾.
的项的假设矛盾.
于是,结论得证.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,短轴长为2.
,短轴长为2.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设P为椭圆上顶点,点A是椭圆C上异于顶点的任意一点,直线![]() 交x轴于点M,点B与点A关于x轴对称,直线
交x轴于点M,点B与点A关于x轴对称,直线![]() 交x轴于点N.问:在y轴的正半轴上是否存在点Q,使得
交x轴于点N.问:在y轴的正半轴上是否存在点Q,使得![]() ?若存在,求点Q的坐标;若不存在,请说明理由.
?若存在,求点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,BB1⊥平面ABC,∠BAC=90°,AC=AB=AA1,E是BC的中点.

(1)求证:AE⊥B1C;
(2)求异面直线AE与A1C所成的角的大小;
(3)若G为C1C中点,求二面角C-AG-E的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
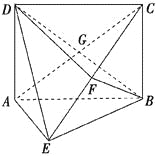
【题目】若四面体![]() 的三组对棱分别相等,即
的三组对棱分别相等,即![]() ,
,![]() ,
,![]() ,给出下列结论:
,给出下列结论:
①四面体![]() 每组对棱相互垂直;
每组对棱相互垂直;
②四面体![]() 每个面的面积相等;
每个面的面积相等;
③从四面体![]() 每个顶点出发的三条棱两两夹角之和大于
每个顶点出发的三条棱两两夹角之和大于![]() 而小于
而小于![]() ;
;
④连接四面体![]() 每组对棱中点的线段相互垂直平分;
每组对棱中点的线段相互垂直平分;
⑤从四面体![]() 每个顶点出发的三条棱的长可作为一个三角形的三边长.
每个顶点出发的三条棱的长可作为一个三角形的三边长.
其中正确结论的个数是( )
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】写出下面平面几何中的常见结论在立体几何中也成立的所有序号______.
①四边形内角和为![]() ;
;
②垂直的两条直线必相交;
③垂直同一条直线的两条直线平行;
④平行同一条直线的两条直线平行;
⑤四边相等的四边形,其对角线垂直;
⑥到三角形三边距离相等的点是这个三角形的内心;
⑦到一个角的两边距离相等的点必在这个角的角平分线上;
⑧在平面几何中有“一组平行线(至少3条)被两条直线所截得的对应线段成比例”的结论,则这一结论可推广到立体几何中“一组平行平面(至少3个)被两条直线所截得的对应线段也成比例.”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.
(1)求证:AE⊥平面BCE;
(2)求证:AE∥平面BFD;
(3)求三棱锥C-BGF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂经过节能降耗技术改进后生产甲产品x吨与相应的生产耗能y吨间的几组数据
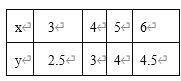
(1)试画出此表中数据对应的散点图 ;
(2)若变量y与x线性相关 ,试求出线性回归方程y = b x + a ;
(3)已知该厂技改前100吨甲产品的生产耗能为90吨标准煤 ,试根据(2)求出的线性回归方程 ,预测生产100吨甲产品的生产耗能比技改前降低多少吨标准煤?
(参考公式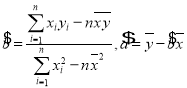 ,)
,)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】五一放假期间高速公路免费是让实惠给老百姓,但也容易造成交通堵塞.在某高速公路上的某时间段内车流量![]() (单位:千辆/小时)与汽车的平均速度
(单位:千辆/小时)与汽车的平均速度![]() (单位:千米/小时)之间满足的函数关系
(单位:千米/小时)之间满足的函数关系![]() (
(![]() 为常数),当汽车的平均速度为
为常数),当汽车的平均速度为![]() 千米/小时时,车流量为
千米/小时时,车流量为![]() 千辆/小时.
千辆/小时.
(1)在该时间段内,当汽车的平均速度![]() 为多少时车流量
为多少时车流量![]() 达到最大值?
达到最大值?
(2)为保证在该时间段内车流量至少为![]() 千辆/小时,则汽车的平均速度应控制在什么范围内?
千辆/小时,则汽车的平均速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型超市在2018年元旦举办了一次抽奖活动,抽奖箱里放有2个红球,1个黄球和1个蓝球(这些小球除颜色外大小形状完全相同),从中随机一次性取2个小球,每位顾客每次抽完奖后将球放回抽奖箱.活动另附说明如下:
①凡购物满100(含100)元者,凭购物打印凭条可获得一次抽奖机会;
②凡购物满188(含188)元者,凭购物打印凭条可获得两次抽奖机会;
③若取得的2个小球都是红球,则该顾客中得一等奖,奖金是一个10元的红包;
④若取得的2个小球都不是红球,则该顾客中得二等奖,奖金是一个5元的红包;
⑤若取得的2个小球只有1个红球,则该顾客中得三等奖,奖金是一个2元的红包.
抽奖活动的组织者记录了该超市前20位顾客的购物消费数据(单位:元),绘制得到如图所示的茎叶图.

(1)求这20位顾客中获得抽奖机会的人数与抽奖总次数(假定每位获得抽奖机会的顾客都会去抽奖);
(2)求这20位顾客中奖得抽奖机会的顾客的购物消费数据的中位数与平均数(结果精确到整数部分);
(3)分别求在一次抽奖中获得红包奖金10元,5元,2元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com