
【题目】已知圆![]() ,直线
,直线![]() ,
, ![]() .
.
(1)求证:对![]() ,直线
,直线![]() 与圆
与圆![]() 总有两个不同的交点
总有两个不同的交点![]() ;
;
(2)求弦![]() 的中点
的中点![]() 的轨迹方程,并说明其轨迹是什么曲线.
的轨迹方程,并说明其轨迹是什么曲线.
【答案】(1)见解析(2) ![]() 的轨迹方程是
的轨迹方程是![]() ,它是一个以
,它是一个以![]() 为圆心,以
为圆心,以![]() 为半径的圆
为半径的圆
【解析】试题分析:(1)利用圆心到直线的距离与圆的半径之间的关系,即可判定直线![]() 与圆
与圆![]() 总有两个不同的交点;
总有两个不同的交点;
(2)设中点为![]() ,当直线
,当直线![]() 的斜率存在时,利用∵
的斜率存在时,利用∵![]() ,化简得
,化简得![]() ;当直线
;当直线![]() 的斜率不存在时,
的斜率不存在时, ![]() ,此时中点为
,此时中点为![]() ,即可得到中点的轨迹方程;
,即可得到中点的轨迹方程;
试题解析:
证明:(1)圆![]() 的圆心为
的圆心为![]() ,半径为
,半径为![]() ,
,
所以圆心![]() 到直线
到直线![]() 的距离
的距离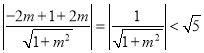 .
.
所以直线![]() 与圆
与圆![]() 相交,即直线
相交,即直线![]() 与圆
与圆![]() 总有两个不同的交点;
总有两个不同的交点;
(2)设中点为![]() ,
,
因为直线![]() 恒过定点
恒过定点![]() ,
,
当直线![]() 的斜率存在时,
的斜率存在时, ![]() ,又
,又![]() ,
,
∵![]() ,∴
,∴![]()
化简得![]() .
.
当直线![]() 的斜率不存在时,
的斜率不存在时, ![]() ,
,
此时中点为![]() ,也满足上述方程.
,也满足上述方程.
所以![]() 的轨迹方程是
的轨迹方程是![]() ,
,
它是一个以![]() 为圆心,以
为圆心,以![]() 为半径的圆.
为半径的圆.


科目:高中数学 来源: 题型:
【题目】如图,在正四棱锥P﹣ABCD中,AB=2,PA= ![]() ,E是棱PC的中点,过AE作平面分别与棱PB、PD交于M、N两点.
,E是棱PC的中点,过AE作平面分别与棱PB、PD交于M、N两点. 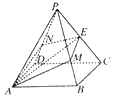
(1)若PM= ![]() PB,PN=λPD,求λ的值;
PB,PN=λPD,求λ的值;
(2)求直线PA与平面AMEN所成角的正弦值的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中, ![]() AD与BC交于点M,设
AD与BC交于点M,设![]() ,以
,以![]() 、
、![]() 为基底表示
为基底表示![]()

【答案】![]()
【解析】试题分析:由A、M、D三点共线,知![]() ;由C、M、B三点共线,知
;由C、M、B三点共线,知![]()
,所以 ,所以
,所以![]() =
=![]() .
.
试题解析:
设![]() ,
,
则![]()
因为A、M、D三点共线,所以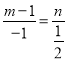 ,即
,即![]()
又![]()
因为C、M、B三点共线,所以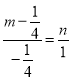 ,即
,即![]()
由![]() 解得
解得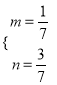 ,所以
,所以![]()
【题型】解答题
【结束】
20
【题目】函数![]() 的最小值为
的最小值为![]() .
.
(1)求![]() ;
;
(2)若![]() ,求
,求![]() 及此时
及此时![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:2a1+22a2+23a3+…+2nan=n(n∈N*),数列{ ![]() }的前n项和为Sn , 则S1S2S3…S10= .
}的前n项和为Sn , 则S1S2S3…S10= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京时间3月10日,CBA半决赛开打,采用7局4胜制(若某对取胜四场,则终止本次比赛,并获得进入决赛资格),采用2﹣3﹣2的赛程,辽宁男篮将与新疆男篮争夺一个决赛名额,由于新疆队常规赛占优,决赛时拥有主场优势(新疆先两个主场,然后三个客场,再两个主场),以下是总决赛赛程:
日期 | 比赛队 | 主场 | 客场 | 比赛时间 | 比赛地点 |
17年3月10日 | 新疆﹣辽宁 | 新疆 | 辽宁 | 20:00 | 乌鲁木齐 |
17年3月12日 | 新疆﹣辽宁 | 新疆 | 辽宁 | 20:00 | 乌鲁木齐 |
17年3月15日 | 辽宁﹣新疆 | 辽宁 | 新疆 | 20:00 | 本溪 |
17年3月17日 | 辽宁﹣新疆 | 辽宁 | 新疆 | 20:00 | 本溪 |
17年3月19日 | 辽宁﹣新疆 | 辽宁 | 新疆 | 20:00 | 本溪 |
17年3月22日 | 新疆﹣辽宁 | 新疆 | 辽宁 | 20:00 | 乌鲁木齐 |
17年3月24日 | 新疆﹣辽宁 | 新疆 | 辽宁 | 20:00 | 乌鲁木齐 |
(1)若考虑主场优势,每个队主场获胜的概率均为 ![]() ,客场取胜的概率均为
,客场取胜的概率均为 ![]() ,求辽宁队以比分4:1获胜的概率;
,求辽宁队以比分4:1获胜的概率;
(2)根据以往资料统计,每场比赛组织者可获得门票收入50万元(与主客场无关),若不考虑主客场因素,每个队每场比赛获胜的概率均为 ![]() ,设本次半决赛中(只考虑这两支队)组织者所获得的门票收入为X,求X的分布列及数学期望.
,设本次半决赛中(只考虑这两支队)组织者所获得的门票收入为X,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学经典名著,它在集合学中的研究比西方早1千年,在《九章算术》中,将四个面均为直角三角形的四面体称为鳖臑,已知某“鳖臑”的三视图如图所示,则该鳖臑的外接球的表面积为( ) 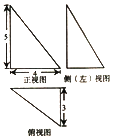
A.200π
B.50π
C.100π
D.![]() π
π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C1的参数方程为 ![]() (θ为参数),曲线 C2的极坐标方程为ρcosθ﹣
(θ为参数),曲线 C2的极坐标方程为ρcosθ﹣ ![]() ρsinθ﹣4=0.
ρsinθ﹣4=0.
(1)求曲线C1的普通方程和曲线 C2的直角坐标方程;
(2)设P为曲线C1上一点,Q为曲线 C2上一点,求|PQ|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业招聘中,依次进行A科、B科考试,当A科合格时,才可考B科,且两科均有一次补考机会,两科都合格方通过.甲参加招聘,已知他每次考A科合格的概率均为 ![]() ,每次考B科合格的概率均为
,每次考B科合格的概率均为 ![]() .假设他不放弃每次考试机会,且每次考试互不影响.
.假设他不放弃每次考试机会,且每次考试互不影响.
(I)求甲恰好3次考试通过的概率;
(II)记甲参加考试的次数为ξ,求ξ的分布列和期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com