【题目】△ABC的内角A，B，C所对的边分别为a，b，c，已知2c﹣a=2bcosA．
（1）求角B的大小；
（2）若 
，求a+c的最大值．
【答案】
（1）解：由已知及正弦定理，得2sinC﹣sinA=2sinBcosA．
∵C=180°﹣A﹣B，
∴2sin（A+B）﹣sinA=2sinBcosA．
化简，得sinA（2cosB﹣1）=0．
∵sinA≠0，
∴ 
．
∵0＜B＜π，
∴ 
．
（2）由已知及正弦定理，得 
．
即a=4sinA，c=4sinC．
从而a+c=4sinA+4sinC，
∵ 
，
∴ 
，
化简得： 
，
∵ 
，
可得 
，
于是 
，
当 
时，
故得a+c的最大值为： 
．
【解析】（1）根据正弦定理进行边角互化，再结合三角恒等变化可求出B的值，（2）根据正弦定理进行边角互化，用角表示出表，进行三角恒等变换，由正弦函数的图象和性质可求出a+c的最大值.
科目：高中数学 来源： 题型：
【题目】某市郊区有一加油站，2018年初汽油的存储量为50吨，计划从年初起每周初均购进汽油
吨，以满足城区内和城外汽车用油需求，已知城外汽车用油每周5吨；城区内汽车用油前
个周需求量
吨与
的函数关系式为
， 
为常数，且前4个周城区内汽车的汽油需求量为100吨.
（1）试写出第
个周结束时，汽油存储量
（吨）与
的函数关系式；
（2）要使16个周内每周按计划购进汽油之后，加油站总能满足城区内和城外的需求，且每周结束时加油站的汽油存储量不超过150吨，试确定
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知△BCD中，∠BCD=90°，BC=CD=1，AB⊥平面BCD，∠ADB=60°，E、F分别是AC、AD上的动点，且 
=λ（0＜λ＜1）．
（Ⅰ）求证：不论λ为何值，总有平面BEF⊥平面ABC；
（Ⅱ）当λ为何值时，平面BEF⊥平面ACD？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知中心在坐标原点的椭圆 
的长轴的一个端点是抛物线 
的焦点，且椭圆 的离心率是 
.
（1）求椭圆 的方程；
（2）过点 
的动直线与椭圆 相交于 
两点.若线段 
的中点的横坐标是 
，求直线 的方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆 
的左、右焦点分别为 
，椭圆 
过点 
，直线 
交 
轴于 
，且 
， 
为坐标原点．
（1）求椭圆 的方程；
（2）设 
是椭圆 的上顶点，过点 分别作直线 
交椭圆 于 
两点，设这两条直线的斜率分别为 
，且 
，证明：直线 
过定点．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数f（x）=sin（ωx﹣ 
）+sin（ωx﹣ 
），其中0＜ω＜3，已知f（ ）=0．
（Ⅰ）求ω；
（Ⅱ）将函数y=f（x）的图象上各点的横坐标伸长为原来的2倍（纵坐标不变），再将得到的图象向左平移 
个单位，得到函数y=g（x）的图象，求g（x）在[﹣ ， 
]上的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】利民中学为了了解该校高一年级学生的数学成绩，从高一年级期中考试成绩中抽出100名学生的成绩，由成绩得到如下的频率分布直方图.
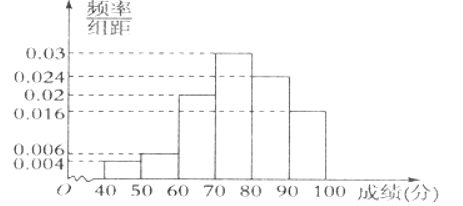
根据以上频率分布直方图，回答下列问题：
（1）求这100名学生成绩的及格率；（大于等于60分为及格）
（2）试比较这100名学生的平均成绩和中位数的大小.（精确到0.1）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】己知直线l1：4x﹣3y+6=0和直线l2：x=﹣1，抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是（ ）
A.2
B.3
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在每年的春节后，某市政府都会发动公务员参与到植树绿化活动中去．林业管理部门在植树前，为了保证树苗的质量，都会在植树前对树苗进行检测．现从甲、乙两种树苗中各抽测了10株树苗，量出它们的高度如下（单位：厘米）：
甲：37，21，31，20，29，19，32，23，25，33；
乙：10，30，47，27，46，14，26，10，44，46．
（1）画出两组数据的茎叶图，并根据茎叶图对甲、乙两种树苗的高度作比较，写出两个统计结论；
（2）设抽测的10株甲种树苗高度平均值为
，将这10株树苗的高度依次输入，按程序框（如图）进行运算，问输出的S大小为多少？并说明S的统计学意义．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com