
 ��֪��ԲC��$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1��{a��b��0}��$���ϡ��½���ֱ�ΪF1��F2���Ͻ���F1��ֱ�� 4x+3y+12=0�ľ���Ϊ3����ԲC��������e=$\frac{1}{2}$��
��֪��ԲC��$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1��{a��b��0}��$���ϡ��½���ֱ�ΪF1��F2���Ͻ���F1��ֱ�� 4x+3y+12=0�ľ���Ϊ3����ԲC��������e=$\frac{1}{2}$������ ��������Բ�Ͻ���F1��0��c������F1��ֱ��4x+3y+12=0�ľ���Ϊ3�������ԲC��������$e=\frac{1}{2}$�������ԲC���̣��Ƴ�1��|PF1|��3����$|{\overrightarrow{P{F_1}}}|=t��|{{{\overrightarrow{PF}}_2}}|=4-t$��$|{\overrightarrow{P{F_1}}}|•|{{{\overrightarrow{PF}}_2}}|=t��4-t��$=-��t-2��2+4��t=2ʱ��Ȼ�����$|{\overrightarrow{P{F_1}}}|•|{{{\overrightarrow{PF}}_2}}|$ȡֵ��Χ��
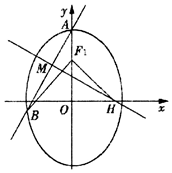
������ֱ��l��б��Ϊk��ֱ��l�ķ���y-2=kx����B��xB��yB����A��xA��yA��������ֱ������Բ���̣����A��B���꣬����$\overrightarrow{{F_1}B}•\overrightarrow{{F_1}H}=0$�����H��M�����꣬�Ƴ�k�������ֱ��l�ķ��̣�
��� ����С������13�֣�
�⣺��������֪��ԲC����Ϊ$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1��a��b��0��$��
����Բ�Ͻ���F1��0��c������F1��ֱ��4x+3y+12=0�ľ���Ϊ3��
��$\frac{{|{3c+12}|}}{5}=3$������ԲC��������$e=\frac{1}{2}$������$\frac{c}{a}=\frac{1}{2}$����a2=b2+c2��
���a2=4?b2=3����ԲC����Ϊ$\frac{y^2}{4}+\frac{x^2}{3}=1$��
����1��|PF1|��3����$|{\overrightarrow{P{F_1}}}|=t��|{{{\overrightarrow{PF}}_2}}|=4-t$��$|{\overrightarrow{P{F_1}}}|•|{{{\overrightarrow{PF}}_2}}|=t��4-t��$=-��t-2��2+4��t=2ʱ��
$|{\overrightarrow{P{F_1}}}|•|{{{\overrightarrow{PF}}_2}}|$���ֵΪ4��t=1��3ʱ��$|{\overrightarrow{P{F_1}}}|•|{{{\overrightarrow{PF}}_2}}|$��СֵΪ3��
$|{\overrightarrow{P{F_1}}}|•|{\overrightarrow{P{F_2}}}|$ȡֵ��Χ��[3��4]������5�֣�
������ֱ��l��б��Ϊk��
��ֱ��l����y-2=kx����B��xB��yB����A��xA��yA����
��$\left\{\begin{array}{l}y=kx+2\\ \frac{y^2}{4}+\frac{x^2}{3}=1\end{array}\right.$���ã�3k2+4��x2+12kx=0��
����xA=0��${x_B}=\frac{-12k}{{3{k^2}+4}}$������${y_B}=\frac{{-6{k^2}+8}}{{3{k^2}+4}}$��
����$\overrightarrow{{F_1}B}=��\frac{-12k}{{3{k^2}+4}}��\frac{{8-6{k^2}}}{{3{k^2}+4}}-1��$��$\overrightarrow{{F_1}H}=��{x_H}��-1��$��
����֪$\overrightarrow{{F_1}B}•\overrightarrow{{F_1}H}=0$��
����$\frac{-12k}{{3{k^2}+4}}•{x_H}$$+1-\frac{{-6{k^2}+8}}{{3{k^2}+4}}=0$�����${x_H}=\frac{{9{k^2}-4}}{12k}$��$|{\overrightarrow{MO}}|=|{\overrightarrow{MA}}|$��
$x_M^2+y_M^2=x_M^2+{��{y_M}-2��^2}$��yM=1��MH�ķ���$y=-\frac{1}{k}��x-\frac{{9{k^2}-4}}{12k}��$������$\left\{\begin{array}{l}y=kx+2\\ y=-\frac{1}{k}��x-\frac{{9{k^2}-4}}{12k}��\end{array}\right.$��
${y_M}=\frac{{9{k^2}+20}}{{12��1+{k^2}��}}=1$�����${k^2}=\frac{8}{3}$��
����ֱ��l�ķ���Ϊ$y=��\frac{{2\sqrt{6}}}{3}x+2$������13�֣�
���� ���⿼��ֱ������Բ��λ�ù�ϵ��Ӧ�ã���Բ���̵���������������������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��2 | B�� | -2 | C�� | 2 | D�� | 0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 2$\sqrt{2}$ | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 5 | C�� | 7 | D�� | 9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{7}{16}$ | B�� | $\frac{5}{8}$ | C�� | $\frac{9}{16}$ | D�� | $\frac{7}{8}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
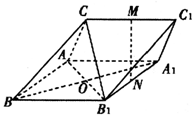 ��ͼ��������ABC-A1B1Cl�У�M��N�ֱ�ΪCC1��A1B1���е㣮CA��CB1��CA=CB1��BA=BC=BB1��
��ͼ��������ABC-A1B1Cl�У�M��N�ֱ�ΪCC1��A1B1���е㣮CA��CB1��CA=CB1��BA=BC=BB1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com