
 的上、下焦点及左、右顶点均在圆O:x2+y2=1上.
的上、下焦点及左、右顶点均在圆O:x2+y2=1上. ,求证:λ1+λ2为定值.
,求证:λ1+λ2为定值. ,若点S满足:
,若点S满足: ,证明:点S在椭圆C2上.
,证明:点S在椭圆C2上.(1)解:由C1:y2=2px(p>0)焦点F( ,0)在圆O:x2+y2=1上得:
,0)在圆O:x2+y2=1上得: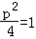 ,
,
∴p=2
∴抛物线C1:y2=4x
同理由椭圆C2: 的上、下焦点(0,c),(0,﹣c)及左、右顶点(﹣b,0),(b,0)均在圆O:x2+y2=1上可解得:b=c=1,a=
的上、下焦点(0,c),(0,﹣c)及左、右顶点(﹣b,0),(b,0)均在圆O:x2+y2=1上可解得:b=c=1,a=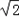
∴椭圆C2: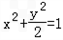
(2)证明:设直线AB的方程为y=k(x﹣1),A(x1,y1),B(x2,y2),则N(0,﹣k)直线与抛物线联立,消元可得
k2x2﹣(2k2+4)x+k2=0
∴x1+x2= ,x1x2=1
,x1x2=1
∵
∴λ1(1﹣x1)=x1,λ2(1﹣x2)=x2
∴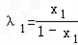 ,
,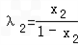
∴λ1+λ2=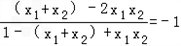 为定值;
为定值;
(3)证明:设P(x3,y3),Q(x4,y4),则P'(x3,0),Q'(x4,0),
∵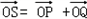 ,
,
∴S(x3+x4,y3+y4)
∵
∴2x3x4+y3y4=﹣1①
∵P,Q在椭圆上,
∴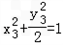 ②,
②, ③
③
由①+②+③得(x3+x4)2+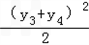 =1
=1
∴点S在椭圆C2上


科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•河北模拟)已知抛物线C1:y2=2px和圆C2:(x-
(2012•河北模拟)已知抛物线C1:y2=2px和圆C2:(x-| p |
| 2 |
| p2 |
| 4 |
| AB |
| CD |
| p2 |
| 4 |
| p2 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| y2 |
| a2 |
| y2 |
| b2 |
| NA |
| AF |
| NB |
| BF |
| OP |
| OQ |
| OP′ |
| OQ′ |
| OS |
| OP |
| OQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
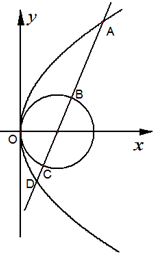 已知抛物线C1:y2=4x,圆C2:(x-1)2+y2=1,过抛物线焦点F的直线l交C1于A,D两点(点A在x轴上方),直线l交C2于B,C两点(点B在x轴上方).
已知抛物线C1:y2=4x,圆C2:(x-1)2+y2=1,过抛物线焦点F的直线l交C1于A,D两点(点A在x轴上方),直线l交C2于B,C两点(点B在x轴上方).| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com